题目内容
已知函数f(x)=x3-3ax2+3x+1.
(1)设a=2,求f(x)的单调区间;
(2)设f(x)在区间(2,3)中至少有一个极值点,求a的取值范围.
(1)设a=2,求f(x)的单调区间;
(2)设f(x)在区间(2,3)中至少有一个极值点,求a的取值范围.
(1)f(x)的递增区间是(-∞,2- )与(2+
)与(2+ ,+∞);
,+∞);
f(x)的递减区间是(2- ,2+
,2+ )
)
(2)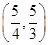
 )与(2+
)与(2+ ,+∞);
,+∞);f(x)的递减区间是(2-
 ,2+
,2+ )
)(2)
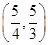
(1)当a=2时,f(x)=x3-6x2+3x+1.
f′(x)=3x2-12x+3
=3(x2-4x+1)
=3(x-2+ )(x-2-
)(x-2- ).
).
当x<2- ,或x>2+
,或x>2+ 时,得f′(x)>0;
时,得f′(x)>0;
当2- <x<2+
<x<2+ 时,得f′(x)<0.
时,得f′(x)<0.
因此f(x)的递增区间是(-∞,2- )与(2+
)与(2+ ,+∞);
,+∞);
f(x)的递减区间是(2- ,2+
,2+ ).
).
(2)f′(x)=3x2-6ax+3,
Δ=36a2-36,由Δ>0得,a>1或a<-1,又x1x2=1,
可知f′(2)<0,且f′(3)>0,
解得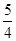 <a<
<a<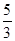 ,
,
因此a的取值范围是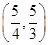 .
.
f′(x)=3x2-12x+3
=3(x2-4x+1)
=3(x-2+
 )(x-2-
)(x-2- ).
).当x<2-
 ,或x>2+
,或x>2+ 时,得f′(x)>0;
时,得f′(x)>0;当2-
 <x<2+
<x<2+ 时,得f′(x)<0.
时,得f′(x)<0.因此f(x)的递增区间是(-∞,2-
 )与(2+
)与(2+ ,+∞);
,+∞);f(x)的递减区间是(2-
 ,2+
,2+ ).
).(2)f′(x)=3x2-6ax+3,
Δ=36a2-36,由Δ>0得,a>1或a<-1,又x1x2=1,
可知f′(2)<0,且f′(3)>0,
解得
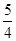 <a<
<a<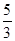 ,
,因此a的取值范围是
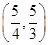 .
.
练习册系列答案
相关题目
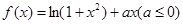
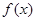 的单调性.
的单调性.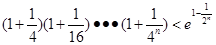 (
(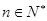 ,e为自然对数的底数)
,e为自然对数的底数) .
. 的单调区间;
的单调区间; 时,求证:
时,求证: 恒成立..
恒成立..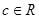 ,且a+b>0,a+c>0,b+c>0,则f(a)+f(b)+f(c)的值( )
,且a+b>0,a+c>0,b+c>0,则f(a)+f(b)+f(c)的值( ) 满足下列条件:
满足下列条件: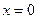 处导数为-1;③在
处导数为-1;③在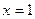 处切线方程为
处切线方程为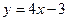 .
.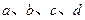 的值;
的值;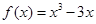 在区间
在区间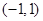 上( )
上( )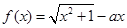
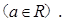
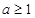 时,函数
时,函数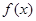 在区间
在区间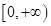 上是单调递减函数;
上是单调递减函数;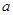 的取值范围,使函数
的取值范围,使函数 都是定义在
都是定义在 上的函数,
上的函数, ,
, ,且
,且 ,
,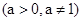 ,
, ,对于数列
,对于数列 ,任取正整数
,任取正整数 ,则前k项和大于
,则前k项和大于 的概率是( )
的概率是( )


