题目内容
设函数f(x)=ln x-p(x-1),p∈R.
(1)当p=1时,求函数f(x)的单调区间;
(2)设函数g(x)=xf(x)+p(2x2-x-1)(x≥1),求证:当p≤-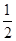 时,有g(x)≤0.
时,有g(x)≤0.
(1)当p=1时,求函数f(x)的单调区间;
(2)设函数g(x)=xf(x)+p(2x2-x-1)(x≥1),求证:当p≤-
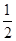 时,有g(x)≤0.
时,有g(x)≤0.(1)f(x)的单调递增区间为(0,1),单调递减区间为(1,+∞).
(2)见解析
(2)见解析
(1)解:当p=1时,f(x)=ln x-x+1,
其定义域为(0,+∞),
∴f′(x)=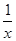 -1,
-1,
由f′(x)=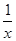 -1>0,得0<x<1,
-1>0,得0<x<1,
由f′(x)<0,得x>1,
∴f(x)的单调递增区间为(0,1),
单调递减区间为(1,+∞).
(2)证明:由函数g(x)=xf(x)+p(2x2-x-1)
=xln x+p(x2-1),
得g′(x)=ln x+1+2px.
由(1)知,当p=1时,f(x)≤f(1)=0,
即不等式ln x≤x-1成立,
所以当p≤-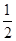 时,g′(x)=ln x+1+2px≤(x-1)+1+2px=(1+2p)x≤0,
时,g′(x)=ln x+1+2px≤(x-1)+1+2px=(1+2p)x≤0,
即g(x)在[1,+∞)上单调递减,
从而g(x)≤g(1)=0满足题意.
其定义域为(0,+∞),
∴f′(x)=
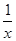 -1,
-1,由f′(x)=
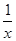 -1>0,得0<x<1,
-1>0,得0<x<1,由f′(x)<0,得x>1,
∴f(x)的单调递增区间为(0,1),
单调递减区间为(1,+∞).
(2)证明:由函数g(x)=xf(x)+p(2x2-x-1)
=xln x+p(x2-1),
得g′(x)=ln x+1+2px.
由(1)知,当p=1时,f(x)≤f(1)=0,
即不等式ln x≤x-1成立,
所以当p≤-
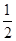 时,g′(x)=ln x+1+2px≤(x-1)+1+2px=(1+2p)x≤0,
时,g′(x)=ln x+1+2px≤(x-1)+1+2px=(1+2p)x≤0,即g(x)在[1,+∞)上单调递减,
从而g(x)≤g(1)=0满足题意.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 满足
满足 (其中
(其中 为
为 处的导数,
处的导数, 为常数).
为常数). ,若函数
,若函数 在
在 上单调,求实数
上单调,求实数 ,且
,且 .
. 的值;
的值; 的单调区间;
的单调区间; ,若函数
,若函数 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围. R,求函数
R,求函数 在区间
在区间 上的最小值.
上的最小值. 是减函数的区间为 ( )
是减函数的区间为 ( )



 .
. 的单调性,并说明理由;
的单调性,并说明理由; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,函数
,函数 ,若
,若 在
在 上是单调减函数,则
上是单调减函数,则 的取值范围是
的取值范围是



 在区间
在区间 上是单调递增函数,则实数
上是单调递增函数,则实数 的取值范围是 .
的取值范围是 .