题目内容
已知函数 满足
满足 (其中
(其中 为
为 在点
在点 处的导数,
处的导数, 为常数).
为常数).
(1)求函数 的单调区间
的单调区间
(2)设函数 ,若函数
,若函数 在
在 上单调,求实数
上单调,求实数 的取值范围.
的取值范围.
 满足
满足 (其中
(其中 为
为 在点
在点 处的导数,
处的导数, 为常数).
为常数).(1)求函数
 的单调区间
的单调区间(2)设函数
 ,若函数
,若函数 在
在 上单调,求实数
上单调,求实数 的取值范围.
的取值范围.(1)详见解析;(2) c ³11或c £ –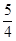
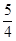
试题分析:(1)将
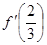 的值代入
的值代入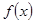 的解析式,列出
的解析式,列出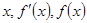 的变化情况表,根据表求出函数
的变化情况表,根据表求出函数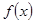 的单调区间.
的单调区间.(2)求出函数
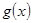 的导数,构造函数
的导数,构造函数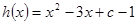 ,分函数递增和递减两类,令
,分函数递增和递减两类,令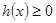 和
和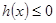 在
在 上恒成立,求出C的范围.
上恒成立,求出C的范围.试题解析:(1)由
 ,得
,得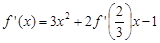 .
.取
 ,得
,得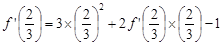 ,
,解之,得
 ,
, 因为
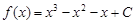 .
.从而
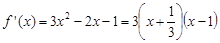 ,列表如下:
,列表如下: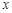 | 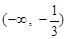 |  | 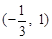 | 1 | 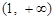 |
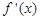 | + | 0 | - | 0 | + |
 | ↗ | 有极大值 | ↘ | 有极小值 | ↗ |
∴
 的单调递增区间是
的单调递增区间是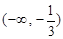 和
和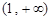 ;
; 的单调递减区间是
的单调递减区间是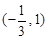 .
. (3)函数
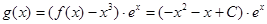 ,
,有
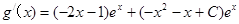 =(–x2– 3 x+C–1)ex,
=(–x2– 3 x+C–1)ex, 当函数在区间
 上为单调递增时,等价于h(x)= –x2– 3 x+C–1³0在
上为单调递增时,等价于h(x)= –x2– 3 x+C–1³0在 上恒成立, 只要h(2)³0,解得c ³11,
上恒成立, 只要h(2)³0,解得c ³11, 当函数在区间
 上为单调递减时,等价于h(x)= –x2– 3 x+C–1£0在
上为单调递减时,等价于h(x)= –x2– 3 x+C–1£0在 上恒成立, 即
上恒成立, 即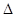 =
=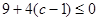 ,解得c £ –
,解得c £ –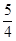 ,
,所以c的取值范围是c ³11或c £ –
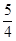 .
. 
练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
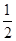 时,有g(x)≤0.
时,有g(x)≤0.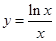 的最大值为( )
的最大值为( )



 在
在 上递增,则
上递增,则 的范围是( )
的范围是( )



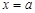 和
和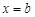 是函数
是函数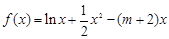 的两个极值点,其中
的两个极值点,其中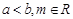 .
.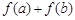 的取值范围;
的取值范围;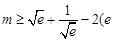 为自然对数的底数),求
为自然对数的底数),求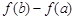 的最大值.
的最大值.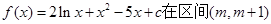 上为递减函数,则m的取值范围是 。
上为递减函数,则m的取值范围是 。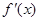 是
是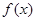 的导函数,
的导函数,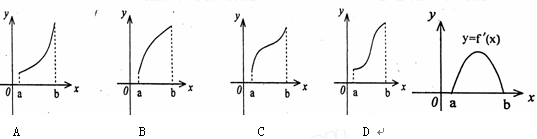
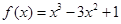 的单调递减区间为( ).
的单调递减区间为( ).