题目内容
18.已知圆O:x2+y2=r2(r>0),与y轴交于M、N两点且M在N的上方.若直线y=2x+$\sqrt{5}$与圆O相切.(1)求实数r的值;
(2)若动点P满足PM=$\sqrt{3}$PN,求△PMN面积的最大值.
(3)设圆O上相异两点A、B满足直线MA、MB的斜率之积为$\frac{\sqrt{3}}{3}$.试探究直线AB是否经过定点,若经过,请求出定点的坐标;若不经过,请说明理由.
分析 (1)由直线和圆相切的条件:d=r,计算即可得到r=1;
(2)设点P(x,y),运用两点的距离公式,化简整理可得P的轨迹为圆,可得点P到y轴的距离最大值为$\sqrt{3}$,再由三角形的面积公式可得最大值;
(3)设A(x1,y1),B(x2,y2),讨论直线AB的斜率不存在和存在,设出直线方程,运用直线的斜率公式计算即可得到m的值,进而判断直线AB是否经过定点.
解答 解:(1)∵直线y=2x+$\sqrt{5}$与圆O相切,
∴圆心O(0,0)到直线2x-y+$\sqrt{5}$=0的距离为d=$\frac{\sqrt{5}}{\sqrt{5}}$=1
∴r=1;
(2)设点P(x,y),点M(0,1),N(0,-1),MN=2;
∵PM=$\sqrt{3}$PN,
∴x2+(y-1)2=3[x2+(y+1)2],即x2+y2+4y+1=0,
∴点P在圆心为(0,-2),半径为$\sqrt{3}$的圆上,
∴点P到y轴的距离最大值为$\sqrt{3}$,
∴△PMN的面积的最大值为$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$.
(3)设A(x1,y1),B(x2,y2),
则x12+y12=1,x22+y22=1,
①若直线AB的斜率不存在,则x1=x2,y1=-y2,则
kMA•kMB=$\frac{{y}_{1}-1}{{x}_{1}}$•$\frac{{y}_{2}-1}{{x}_{2}}$=$\frac{-{y}_{2}-1}{{x}_{2}}$•$\frac{{y}_{2}-1}{{x}_{2}}$=$\frac{1-{{y}_{2}}^{2}}{{{x}_{2}}^{2}}$=1
与直线MA、MB的斜率之积为$\frac{\sqrt{3}}{3}$矛盾;
②设直线AB:y=kx+m,则$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$
∴(1+k2)x2+2kmx+m2-1=0,
∴x1+x2=-$\frac{2km}{{k}^{2}+1}$,x1x2=$\frac{{m}^{2}-1}{1+{k}^{2}}$,
则y1+y2=$\frac{2m}{{k}^{2}+1}$,y1y2=$\frac{{m}^{2}-{k}^{2}}{{k}^{2}+1}$,
∵kMA•kMB=$\frac{\sqrt{3}}{3}$
∴$\frac{{y}_{1}-1}{{x}_{1}}$•$\frac{{y}_{2}-1}{{x}_{2}}$=$\frac{{y}_{1}{y}_{2}-({y}_{1}+{y}_{2})+1}{{x}_{1}{x}_{2}}$=$\frac{\frac{{m}^{2}-{k}^{2}}{1+{k}^{2}}-\frac{2m}{1+{k}^{2}}+1}{\frac{{m}^{2}-1}{{k}^{2}+1}}$=$\frac{\sqrt{3}}{3}$
化简得:$\frac{m-1}{m+1}$=$\frac{1}{\sqrt{3}}$,解得m=2+$\sqrt{3}$,
∴直线AB过定点(0,2+$\sqrt{3}$).
综上:直线AB过定点(0,2+$\sqrt{3}$).
点评 本题考查直线和圆的位置关系:相切和相交,考查圆的方程的求法和直线方程联立圆的方程,运用韦达定理,以及直线的斜率公式,属于中档题.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案| A. | 抛物线 | B. | 椭圆 | C. | 双曲线 | D. | 圆 |
| A. | $({\frac{π}{4},\frac{π}{3}})$ | B. | $({\frac{2π}{3},\frac{5π}{6}})$ | C. | $({0,\frac{π}{3}})∪({\frac{3π}{4},π})$ | D. | $({\frac{π}{3},\frac{2π}{3}})$ |
| A. | ±8 | B. | 4 | C. | 8 | D. | 64 |
| 零售价x(元/瓶) | 3.0 | 3.2 | 3.4 | 3.6 | 3.8 | 4.0 |
| 销量y(瓶) | 50 | 44 | 43 | 40 | 35 | 28 |
| A. | 39 | B. | 38 | C. | 37 | D. | 36 |
 如图,已知圆O上的弦AC=BD,过点C作圆O的切线与BA的延长线相交于点E
如图,已知圆O上的弦AC=BD,过点C作圆O的切线与BA的延长线相交于点E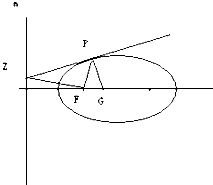 已知:如图,设P为椭圆上的任意一点,过点P作椭圆的切线,交准线m于点Z,此时FZ⊥FP,过点P作PZ的垂线交椭圆的长轴于点G,椭圆的离心率为e,求证:FG=e•FP.
已知:如图,设P为椭圆上的任意一点,过点P作椭圆的切线,交准线m于点Z,此时FZ⊥FP,过点P作PZ的垂线交椭圆的长轴于点G,椭圆的离心率为e,求证:FG=e•FP.