题目内容
3.函数f(x)=ex(sinx-2)在区间[0,2π]上的最大值是( )| A. | -2 | B. | -2e2π | C. | -2eπ | D. | -${e}^{\frac{π}{2}}$ |
分析 求出f(x)的导数,由正弦函数的值域可得f(x)在区间[0,2π]上单调递减,即可得到f(x)的最大值.
解答 解:∵f′(x)=ex(sinx-2)+ex(cosx)
=ex(sinx+cosx-2)=ex[$\sqrt{2}$sin(x+$\frac{π}{4}$)-2]<0,
∴f(x)在区间[0,2π]上单调递减,
∴f(x)max=f(0)=-2.
故选A.
点评 本题考查导数的应用:求最值,同时考查正弦函数的值域,正确求导是解题的关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.函数f(x)=x3+ax2+3x-9已知f(x)在x=-3时取得极值,则a=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
11.设x,y满足约束条件$\left\{\begin{array}{l}3x-y-6≤0\\ x-y+2≥0\\ x≥0,y≥0\end{array}\right.$,若目标函数z=ax+by(a>0,b>0)的最大值为36,则$\frac{2}{a}+\frac{3}{b}$的最小值为( )
| A. | $\frac{25}{18}$ | B. | $\frac{25}{9}$ | C. | $\frac{25}{3}$ | D. | $\frac{50}{18}$ |
18.已知随机变量ξ服从正态分布N(1,σ2).若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为( )
| A. | 0.8 | B. | 0.6 | C. | 0.5 | D. | 0.4 |
12.若函数f(x)=(m-2)x2+(m2-1)x+1是偶函数,则在区间(-∞,0]上,f(x)是( )
| A. | 增函数 | B. | 减函数 | ||
| C. | 常数函数 | D. | 可能是增函数,也可能是常数函数 |
 如图,已知圆O上的弦AC=BD,过点C作圆O的切线与BA的延长线相交于点E
如图,已知圆O上的弦AC=BD,过点C作圆O的切线与BA的延长线相交于点E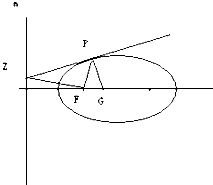 已知:如图,设P为椭圆上的任意一点,过点P作椭圆的切线,交准线m于点Z,此时FZ⊥FP,过点P作PZ的垂线交椭圆的长轴于点G,椭圆的离心率为e,求证:FG=e•FP.
已知:如图,设P为椭圆上的任意一点,过点P作椭圆的切线,交准线m于点Z,此时FZ⊥FP,过点P作PZ的垂线交椭圆的长轴于点G,椭圆的离心率为e,求证:FG=e•FP.