题目内容
4.已知函数f(x)=ax+$\frac{b}{x}$+c(a>0),g(x)=lnx,其中函数f(x)的图象在点(1,f(1))处的切线方程为y=x-1.(Ⅰ)若a=1,求函数f(x)的解析式;
(Ⅱ)若f(x)≥g(x)在[1,+∞)上恒成立,求实数a的取值范围;
(Ⅲ)证明:1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}>ln(n+1)+\frac{n}{2(n+1)}$(n≥1).
分析 (Ⅰ)求导数,利用函数f(x)的图象在点(1,f(1))处的切线方程为y=x-1,求函数f(x)的解析式;
(Ⅱ)若f(x)≥g(x)在[1,+∞)上恒成立,构造新函数,分类讨论,确定函数的单调性,即可求实数a的取值范围;
(Ⅲ)证明一:令$a=\frac{1}{2}$,有$f(x)=\frac{1}{2}({x-\frac{1}{x}})$≥lnx且当x>1时,$\frac{1}{2}({x-\frac{1}{x}})$>lnx. 令$x=\frac{k+1}{k}$,再利用累加法,即可证明;证明二,用数学归纳法证明.
解答 (Ⅰ)解:求导数${f^'}(x)=a-\frac{b}{x^2}$,则有$\left\{{\begin{array}{l}{f(1)=a+b+c=0}\\{f'(1)=a-b=1}\end{array}}\right.$,
解得$\left\{{\begin{array}{l}{b=0}\\{c=-1}\end{array}}\right.$,∴f(x)=x-1;
(Ⅱ)解:由(Ⅰ)知$f(x)=ax+\frac{a-1}{x}+1-2a$,
令$φ(x)=f(x)-g(x)=ax+\frac{a-1}{x}+1-2a-lnx$,x∈[1,+∞),则$φ(1)=0,{φ^'}(x)=a-\frac{a-1}{x^2}-\frac{1}{x}=\frac{{a{x^2}-x-({a-1})}}{x^2}=\frac{{a({x-1})({x-\frac{1-a}{a}})}}{x^2}$,
( i)当$0<a<\frac{1}{2}$时,$\frac{1-a}{a}>1$.
若$1<x<\frac{1-a}{a}$,则φ′(x)<0,φ(x)是减函数,
所以φ(x)<φ(1)=0,即f(x)<g(x).
故f(x)≥g(x)在[1,+∞)上不恒成立.
( ii)当$a≥\frac{1}{2}$时,$\frac{1-a}{a}≤1$.
若x>1,则φ'(x)>0,φ(x)是增函数,
所以φ(x)>φ(1)=0,即f(x)>g(x),故当x≥1时,f(x)≥g(x).
综上所述,所求a的取值范围为$[{\frac{1}{2},+∞})$.
(Ⅲ)解法一:由(Ⅱ)知当$a≥\frac{1}{2}$时,有f(x)≥g(x)(x≥1).
令$a=\frac{1}{2}$,有$f(x)=\frac{1}{2}({x-\frac{1}{x}})$≥lnx且当x>1时,$\frac{1}{2}({x-\frac{1}{x}})$>lnx.
令$x=\frac{k+1}{k}$,有$ln\frac{k+1}{k}<\frac{1}{2}(\frac{k+1}{k}-\frac{k}{k+1})=\frac{1}{2}[{(1+\frac{1}{k})-(1-\frac{1}{k+1})}]$
∴$ln(k+1)-lnk<\frac{1}{2}({\frac{1}{k}+\frac{1}{k+1}}),k=1,2,3,…,n$,
将上述n个不等式依次相加,得$ln({n+1})<\frac{1}{2}+({\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}})+\frac{1}{{2({n+1})}}$,
整理得$1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}>ln({n+1})+\frac{n}{{2({n+1})}}$
解法二:用数学归纳法证明.
①当n=1时,左边=1,右边=$ln2+\frac{1}{4}<1$,不等式成立.
②假设当n=k时,不等式成立,就是$1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{k}>ln({k+1})+\frac{k}{{2({k+1})}}$
那么$1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{k}+\frac{1}{k+1}>ln({k+1})+\frac{k}{{2({k+1})}}+\frac{1}{k+1}$=$ln({k+1})+\frac{k+2}{{2({k+1})}}$
由(Ⅱ)知,当$a≥\frac{1}{2}$时,有f(x)≥lnx(x≥1).
令$a=\frac{1}{2}$,有$f(x)=\frac{1}{2}({x-\frac{1}{x}})≥lnx({x≥1})$.
令$x=\frac{k+2}{k+1}$,得$\frac{1}{2}({\frac{k+2}{k+1}-\frac{k+1}{k+2}})≥ln\frac{k+2}{k+1}=ln({k+2})-ln({k+1})$.
∴$ln({k+1})+\frac{k+2}{{2({k+1})}}≥ln({k+2})+\frac{k+1}{2(k+2)}$.
∴$1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{k}+\frac{1}{k+1}>ln({k+2})+\frac{k+1}{{2({k+2})}}$.
这就是说,当n=k+1时,不等式也成立
根据 ①和 ②,可知不等式对任何n∈N+都成立.
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查不等式的证明,考查学生分析解决问题的能力,有难度.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | 增函数 | B. | 减函数 | ||
| C. | 常数函数 | D. | 可能是增函数,也可能是常数函数 |
| A. | 抛物线 | B. | 椭圆 | C. | 双曲线 | D. | 圆 |
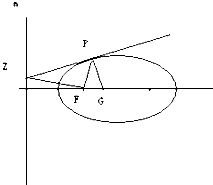 已知:如图,设P为椭圆上的任意一点,过点P作椭圆的切线,交准线m于点Z,此时FZ⊥FP,过点P作PZ的垂线交椭圆的长轴于点G,椭圆的离心率为e,求证:FG=e•FP.
已知:如图,设P为椭圆上的任意一点,过点P作椭圆的切线,交准线m于点Z,此时FZ⊥FP,过点P作PZ的垂线交椭圆的长轴于点G,椭圆的离心率为e,求证:FG=e•FP. 如图,已知PA是⊙O的切线,A是切点,直线PO交⊙O于B、C两点,D是OC的中点,连结AD并延长交⊙O于点E,若PA=2$\sqrt{3}$,∠APB=30°.
如图,已知PA是⊙O的切线,A是切点,直线PO交⊙O于B、C两点,D是OC的中点,连结AD并延长交⊙O于点E,若PA=2$\sqrt{3}$,∠APB=30°.