题目内容
2.已知复数z与(z-3)2+12i都是纯虚数,求z.分析 根据纯虚数的概念以及复数的基本运行进行求解即可.
解答 解:∵z是纯虚数,
∴设z=bi,(b≠0),
则(z-3)2+12i=(bi-3)2+12i=9-b2-6bi+12i=9-b2+(12-6b)i,
若(z-3)2+12i是纯虚数,
则9-b2=0,解得b=±3,
即z=±3i
点评 本题主要考查复数的基本概念,利用待定系数法是解决本题的关键.

练习册系列答案
相关题目
12.若函数f(x)=(m-2)x2+(m2-1)x+1是偶函数,则在区间(-∞,0]上,f(x)是( )
| A. | 增函数 | B. | 减函数 | ||
| C. | 常数函数 | D. | 可能是增函数,也可能是常数函数 |
11.若$cos(\frac{π}{6}-α)=m,(|m|≤1)$,则$sin(\frac{2π}{3}-α)$的值为( )
| A. | -m | B. | $-\frac{m}{2}$ | C. | $\frac{m}{2}$ | D. | m |
12.极坐标方程ρcosθ=2sin2θ表示的曲线为( )
| A. | 一条射线和一个圆 | B. | 一条直线和一个圆 | ||
| C. | 两条直线 | D. | 一个圆 |
 已知:如图,设P为椭圆上的任意一点,过点P作椭圆的切线,交准线m于点Z,此时FZ⊥FP,过点P作PZ的垂线交椭圆的长轴于点G,椭圆的离心率为e,求证:FG=e•FP.
已知:如图,设P为椭圆上的任意一点,过点P作椭圆的切线,交准线m于点Z,此时FZ⊥FP,过点P作PZ的垂线交椭圆的长轴于点G,椭圆的离心率为e,求证:FG=e•FP.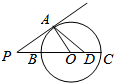 如图,已知PA是⊙O的切线,A是切点,直线PO交⊙O于B、C两点,D是OC的中点,连结AD并延长交⊙O于点E,若PA=2$\sqrt{3}$,∠APB=30°.
如图,已知PA是⊙O的切线,A是切点,直线PO交⊙O于B、C两点,D是OC的中点,连结AD并延长交⊙O于点E,若PA=2$\sqrt{3}$,∠APB=30°.