题目内容
8.已知直线l的方程为:(2+m)x+(1-2m)y+(4-3m)=0.(1)求证:不论m为何值,直线必过定点M;
(2)过点M引直线l1,使它与两坐标轴的负半轴所围成的三角形面积最小,求l1的方程.
分析 (1)原方程整理得:(x-2y-3)m+2x+y+4=0.由$\left\{\begin{array}{l}{x-2y-3=0}\\{2x+y+4=0}\end{array}\right.$,可得直线必过定点M;
(2)表示出面积,利用基本不等式,即可得出结论.
解答 (1)证明:原方程整理得:(x-2y-3)m+2x+y+4=0.
由$\left\{\begin{array}{l}{x-2y-3=0}\\{2x+y+4=0}\end{array}\right.$,可得$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,
∴不论m为何值,直线必过定点M(-1,-2)
(2)解:设直线l1的方程为.y=k(x+1)-2(k<0).
令$y=0,x=\frac{k-2}{-k},令x=0,y=k-2$.
∴${S_△}=\frac{1}{2}|\frac{k-2}{-k}||k-2|=\frac{1}{2}[(-k)+\frac{4}{-k}+4]≥\frac{1}{2}(4+4)=4$.
当且仅当$-k=\frac{4}{-k}$,即k=-2时,三角形面积最小.
则l1的方程为2x+y+4=0.
点评 本题考查直线过定点,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
18.已知随机变量ξ服从正态分布N(1,σ2).若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为( )
| A. | 0.8 | B. | 0.6 | C. | 0.5 | D. | 0.4 |
20.已知圆C:(x-1)2+y2=1,直线l:x+2y-5=0,点P(x0,y0)在直线l上,若存在圆C上的两点M,N,使得∠MPN=60°,则x0的取值范围是( )
| A. | [1,2] | B. | $[{1,\frac{13}{5}}]$ | C. | $[{\frac{1}{2},2}]$ | D. | $[{\frac{1}{2},\frac{13}{5}}]$ |
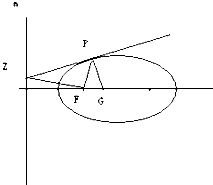 已知:如图,设P为椭圆上的任意一点,过点P作椭圆的切线,交准线m于点Z,此时FZ⊥FP,过点P作PZ的垂线交椭圆的长轴于点G,椭圆的离心率为e,求证:FG=e•FP.
已知:如图,设P为椭圆上的任意一点,过点P作椭圆的切线,交准线m于点Z,此时FZ⊥FP,过点P作PZ的垂线交椭圆的长轴于点G,椭圆的离心率为e,求证:FG=e•FP.