题目内容
已知函数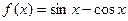 ,
,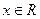 .(1)求函数
.(1)求函数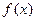 在
在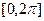 内的单调递增区间;
内的单调递增区间;
(2)若函数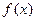 在
在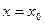 处取到最大值,求
处取到最大值,求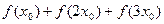 的值;
的值;
(3)若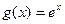 (
(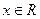 ),求证:方程
),求证:方程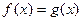 在
在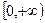 内没有实数解.(参考数据:
内没有实数解.(参考数据: ,
,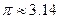 )
)
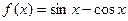 ,
,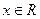 .(1)求函数
.(1)求函数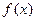 在
在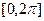 内的单调递增区间;
内的单调递增区间;(2)若函数
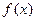 在
在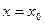 处取到最大值,求
处取到最大值,求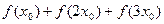 的值;
的值;(3)若
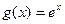 (
(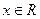 ),求证:方程
),求证:方程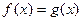 在
在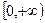 内没有实数解.(参考数据:
内没有实数解.(参考数据: ,
,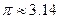 )
)(Ⅰ) 递增区间为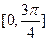 和
和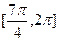 (Ⅱ)
(Ⅱ) 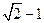 (Ⅲ)见解析
(Ⅲ)见解析
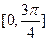 和
和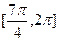 (Ⅱ)
(Ⅱ) 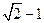 (Ⅲ)见解析
(Ⅲ)见解析(1)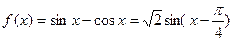 ,令
,令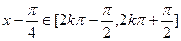 (
(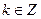 )
)
则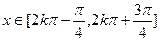 ,----------------2分
,----------------2分
由于 ,则
,则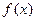 在
在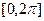 内的单调递增区间为
内的单调递增区间为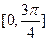 和
和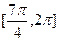 ;
;
---------------4分
(注:将单调递增区间写成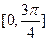
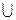
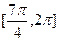 的形式扣1分)
的形式扣1分)
(2)依题意,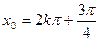 (
(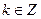 ),-------6分由周期性,
),-------6分由周期性,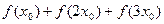
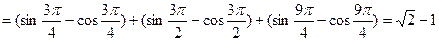 ;-----------------8分
;-----------------8分
(3)函数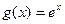 (
(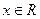 )为单调增函数,
)为单调增函数,
且当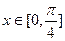 时,
时,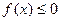 ,
,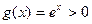 ,此时有
,此时有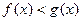 ;-------------10分
;-------------10分
当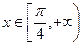 时,由于
时,由于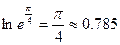 ,而
,而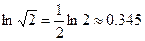 ,
,
则有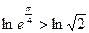 ,即
,即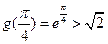 ,
,
又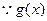 为增函数,
为增函数,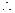 当
当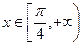 时,
时,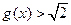 ------12分
------12分
而函数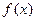 的最大值为
的最大值为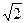 ,即
,即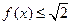 ,则当
,则当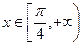 时,恒有
时,恒有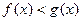 ,
,
综上,在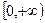 恒有
恒有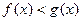 ,即方程
,即方程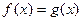 在
在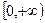 内没有实数解.
内没有实数解.
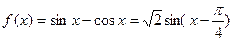 ,令
,令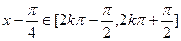 (
(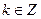 )
)则
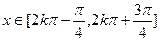 ,----------------2分
,----------------2分由于
 ,则
,则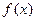 在
在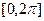 内的单调递增区间为
内的单调递增区间为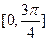 和
和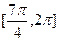 ;
;---------------4分
(注:将单调递增区间写成
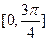
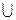
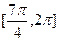 的形式扣1分)
的形式扣1分)(2)依题意,
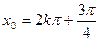 (
(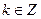 ),-------6分由周期性,
),-------6分由周期性,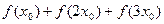
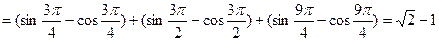 ;-----------------8分
;-----------------8分(3)函数
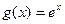 (
(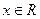 )为单调增函数,
)为单调增函数,且当
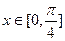 时,
时,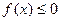 ,
,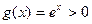 ,此时有
,此时有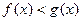 ;-------------10分
;-------------10分当
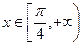 时,由于
时,由于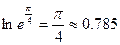 ,而
,而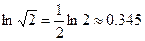 ,
,则有
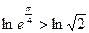 ,即
,即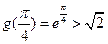 ,
,又
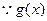 为增函数,
为增函数,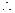 当
当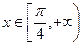 时,
时,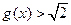 ------12分
------12分而函数
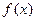 的最大值为
的最大值为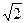 ,即
,即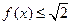 ,则当
,则当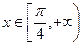 时,恒有
时,恒有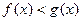 ,
,综上,在
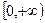 恒有
恒有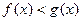 ,即方程
,即方程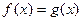 在
在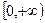 内没有实数解.
内没有实数解.
练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
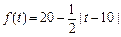 (元).
(元).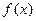 满足
满足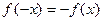 ,函数
,函数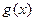 满足
满足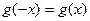 ,且对任意
,且对任意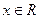 有
有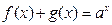 (
(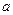 >0,且
>0,且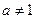 )
)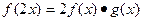 ;
;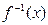 ,当
,当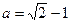 时,试比较
时,试比较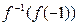 与
与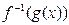 的大小
的大小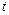 元(其中
元(其中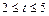 ),设该工厂每件玩具的出厂价为
),设该工厂每件玩具的出厂价为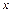 元(
元(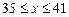 ),根据市场调查,日销售量与
),根据市场调查,日销售量与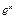 (
(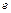 为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.
为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件. (元)与每件玩具的出厂价
(元)与每件玩具的出厂价 最大,并求
最大,并求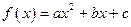 .
. ,试判断函数
,试判断函数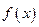 零点个数;
零点个数;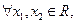 且
且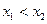 ,
,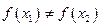 ,试证明
,试证明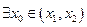 ,使
,使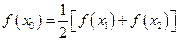 成立。
成立。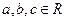 ,使
,使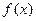 同时满足以下条件①对
同时满足以下条件①对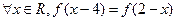 ,且
,且 ;②对
;②对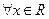 ,都有
,都有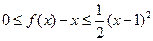 。若存在,求出
。若存在,求出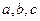 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。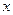 艘产值函数为
艘产值函数为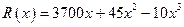 (单位:万元),成本函数
(单位:万元),成本函数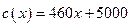 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数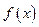 的边际函数
的边际函数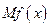 定义为
定义为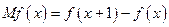
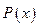 及边际利润函数
及边际利润函数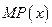 (利润=产值—成本)
(利润=产值—成本)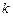 和
和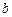 ,使得函数
,使得函数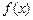 和
和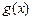 对其定义域上的任意实数
对其定义域上的任意实数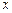 分别满足:
分别满足: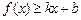 和
和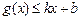 ,则称直线
,则称直线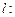
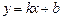 为
为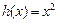 ,
,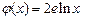 (其中
(其中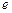 为自然对数的底数),根据你的数学知识,推断
为自然对数的底数),根据你的数学知识,推断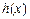 与
与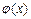 间的隔离直线方程为 .
间的隔离直线方程为 .