题目内容
已知圆心角为120°的扇形AOB的半径为1,C为弧AB的中点,点D、E分别在半径OA、OB上.若CD2+CE2+DE2=
,则OD+OE的最大值是______.
| 26 |
| 9 |
设OD=a,OE=b,由余弦定理,得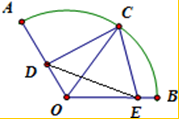 CD2=CO2+DO2-2CO•DOcos60°=a2-a+1.
CD2=CO2+DO2-2CO•DOcos60°=a2-a+1.
同理可得CE2=b2-b+1,DE2=a2+ab+b2
从而得到CD2+CE2+DE2=2(a2+b2)-(a+b)+ab+2=
∴2(a2+b2)-(a+b)+ab-
=0,
配方得2(a+b)2-(a+b)-3ab-
=0,即3ab=2(a+b)2-(a+b)-
…(*)
又∵ab≤[
(a+b)]2=
(a+b)2,
∴3ab≤
(a+b)2,代入(*)式,得2(a+b)2-(a+b)-
≤
(a+b)2,
设a+b=m,代入上式有2m2-m-
≤
m2,
即
m2-m-
≤0,得到-
≤m≤
,
∴m最大值为
,即OD+OE的最大值是
.
 CD2=CO2+DO2-2CO•DOcos60°=a2-a+1.
CD2=CO2+DO2-2CO•DOcos60°=a2-a+1.同理可得CE2=b2-b+1,DE2=a2+ab+b2
从而得到CD2+CE2+DE2=2(a2+b2)-(a+b)+ab+2=
| 26 |
| 9 |
∴2(a2+b2)-(a+b)+ab-
| 8 |
| 9 |
配方得2(a+b)2-(a+b)-3ab-
| 8 |
| 9 |
| 8 |
| 9 |
又∵ab≤[
| 1 |
| 2 |
| 1 |
| 4 |
∴3ab≤
| 3 |
| 4 |
| 8 |
| 9 |
| 3 |
| 4 |
设a+b=m,代入上式有2m2-m-
| 8 |
| 9 |
| 3 |
| 4 |
即
| 5 |
| 4 |
| 8 |
| 9 |
| 8 |
| 15 |
| 4 |
| 3 |
∴m最大值为
| 4 |
| 3 |
| 4 |
| 3 |

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 m,一艘船从
m,一艘船从 处出发到河对岸.已知船的速度
处出发到河对岸.已知船的速度 km/h,水流速度
km/h,水流速度 km/h.要使船行驶的时间最短,那么船行驶的距离与合速度的比值必须最小.此时我们分三种情况讨论:
km/h.要使船行驶的时间最短,那么船行驶的距离与合速度的比值必须最小.此时我们分三种情况讨论: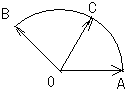


 ,则点M的轨迹方程为
,则点M的轨迹方程为