题目内容
已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足
=
,点T(-1,1)在AC边所在直线上且满足
•
=0.
(1)求AC边所在直线的方程;
(2)求△ABC外接圆的方程;
(3)若动圆P过点N(-2,0),且与△ABC的外接圆外切,求动圆P的圆心的轨迹方程.

| BM |
| MC |
| AT |
| AB |
(1)求AC边所在直线的方程;
(2)求△ABC外接圆的方程;
(3)若动圆P过点N(-2,0),且与△ABC的外接圆外切,求动圆P的圆心的轨迹方程.

(1)∵
•
=0
∴AT⊥AB,又T在AC上
∴AC⊥AB,△ABC为Rt△ABC,
又AB边所在直线的方程为x-3y-6=0,所以直线AC的斜率为-3.
又因为点T(-1,1)在直线AC上,
所以AC边所在直线的方程为y-1=-3(x+1).即3x+y+2=0.
(2)AC与AB的交点为A,所以由
解得点A的坐标为(0,-2),
∵
=
∴M(2,0)为Rt△ABC的外接圆的圆心
又r=|AM|=
=2
.
从△ABC外接圆的方程为:(x-2)2+y2=8.
(3)因为动圆P过点N,所以|PN|是该圆的半径,又因为动圆P与圆M外切,
所以|PM|=|PN|+2
,即|PM|-|PN|=2
.
故点P的轨迹是以M,N为焦点,实轴长为2
的双曲线的左支.
因为实半轴长a=
,半焦距c=2.所以虚半轴长b=
=
.
从而动圆P的圆心的轨迹方程为
-
=1(x≤-
).
| AT |
| AB |
∴AT⊥AB,又T在AC上
∴AC⊥AB,△ABC为Rt△ABC,
又AB边所在直线的方程为x-3y-6=0,所以直线AC的斜率为-3.
又因为点T(-1,1)在直线AC上,
所以AC边所在直线的方程为y-1=-3(x+1).即3x+y+2=0.
(2)AC与AB的交点为A,所以由
|
∵
| BM |
| MC |
∴M(2,0)为Rt△ABC的外接圆的圆心
又r=|AM|=
| (2-0)2+(0+2)2 |
| 2 |
从△ABC外接圆的方程为:(x-2)2+y2=8.
(3)因为动圆P过点N,所以|PN|是该圆的半径,又因为动圆P与圆M外切,
所以|PM|=|PN|+2
| 2 |
| 2 |
故点P的轨迹是以M,N为焦点,实轴长为2
| 2 |
因为实半轴长a=
| 2 |
| c2-a2 |
| 2 |
从而动圆P的圆心的轨迹方程为
| x2 |
| 2 |
| y2 |
| 2 |
| 2 |

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
 是曲线
是曲线 上的任一点,
上的任一点, 是曲线
是曲线 上的任一点,称
上的任一点,称 的最小值为曲线
的最小值为曲线 与直线
与直线 的距离;
的距离; (
( )的距离为
)的距离为 ,直线
,直线 ,求
,求 的最小值.
的最小值.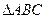 中,
中,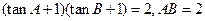 ,求:
,求: 的度数;
的度数;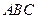 面积的最大值
面积的最大值 与双曲线
与双曲线 有相同的焦点,则a的值是( )
有相同的焦点,则a的值是( )
 . (1)求圆C的方程。(2)点P(x,y)是圆C上的动点,求x+y的最大值。(3)求过点M(2,1)的圆的弦的中点轨迹方程。
. (1)求圆C的方程。(2)点P(x,y)是圆C上的动点,求x+y的最大值。(3)求过点M(2,1)的圆的弦的中点轨迹方程。 和圆O2:
和圆O2:  的位置关系是( )
的位置关系是( )