题目内容
给定两个长度为1的平面向量
和
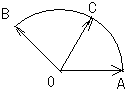
,它们的夹角为120°.如图所示,点C在以O为圆心,以1半径的圆弧AB上变动.若
=x
+y
,其中x,y∈R,则x+y的最大值是______.
| OA |
| OB |
| OC |
| OA |
| OB |

建立如图所示的坐标系,
则A(1,0),B(cos120°,sin120°),
即B(-
,
).
设∠AOC=α,则
=(cosα,sinα).
∵
=x
+y
=(x,0)+(-
,
y)
=(cosα,sinα).
∴
∴x+y=
sinα+cosα=2sin(α+30°).
∵0°≤α≤120°.∴30°≤α+30°≤150°.
∴x+y有最大值2,当α=60°时取最大值2.答案:2

则A(1,0),B(cos120°,sin120°),
即B(-
| 1 |
| 2 |
| ||
| 2 |
设∠AOC=α,则
| OC |
∵
| OC |
| OA |
| OB |
| y |
| 2 |
| ||
| 2 |
=(cosα,sinα).
|
∴
|
∴x+y=
| 3 |
∵0°≤α≤120°.∴30°≤α+30°≤150°.
∴x+y有最大值2,当α=60°时取最大值2.答案:2


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是曲线
是曲线 上的任一点,
上的任一点, 是曲线
是曲线 上的任一点,称
上的任一点,称 的最小值为曲线
的最小值为曲线 与直线
与直线 的距离;
的距离; (
( )的距离为
)的距离为 ,直线
,直线 ,求
,求 的最小值.
的最小值.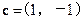 ,b·c=4,则b=____________.
,b·c=4,则b=____________. :
: 与直线
与直线 交于
交于 两点,
两点, 是线段
是线段 的中点,过
的中点,过 轴的垂线,垂足为
轴的垂线,垂足为 ,若
,若 ,则
,则 =
=