题目内容
18.某几何体的三视图如图所示,则该几何体的体积为( )
| A. | $2\sqrt{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | 4 |
分析 由已知中的三视图,可知该几何体是一个以俯视图为底面的三棱柱,切去一个同底等高的三棱锥所得的组合体,分别求出柱体和锥体的体积,相减可得答案.
解答 解:由已知中的三视图,可知该几何体是一个以俯视图为底面的三棱柱,切去一个同底等高的三棱锥所得的组合体,
其三视图如下图所示:
故该几何体的体积为:(1-$\frac{1}{3}$)×$\frac{1}{2}$×2×2×2=$\frac{8}{3}$,
故选:C.
点评 本题考查的知识点是简单空间图象的三视图,其中根据已知中的视图分析出几何体的形状及棱长是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知抛物线x2=-4$\sqrt{5}$y的焦点与双曲线$\frac{x^2}{a}+\frac{y^2}{4}$=1(a∈R)的一焦点重合,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{{5\sqrt{3}}}{3}$ | D. | $\frac{{3\sqrt{5}}}{5}$ |
7.直线l:8x-6y-3=0被圆O:x2+y2-2x+a=0所截得弦的长度为$\sqrt{3}$,则实数a的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 1-$\frac{{\sqrt{13}}}{2}$ |
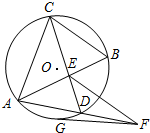 如图,已知圆O的两弦AB和CD相交于点E,FG是圆O的切线,G为切点,EF=FG.
如图,已知圆O的两弦AB和CD相交于点E,FG是圆O的切线,G为切点,EF=FG.