Question

13．已知函数f（x）=|lg|x-$\frac{10}{3}$||，若关于x的方程f²（x）-5f（x）-6=0的实根之和为m，则f（m）的值是1．

Answer 1

分析 根据一元二次方程求出f（x）=6，作出函数f（x）的图象，判断函数f（x）的对称性，即可求出m的值．

解答 解：由f²（x）-5f（x）-6=0得[f（x）-6][f（x）+1]=0，
即f（x）=6或f（x）=-1，
∵f（x）=|lg|x-$\frac{10}{3}$||，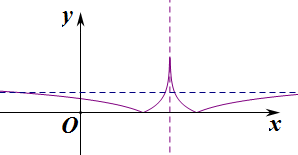
∴f（x）=-1不成立，
故f（x）=6，
作出函数f（x）的图象，
则函数f（x）关于x=$\frac{10}{3}$对称，
由f（x）=6，得方程有四个根，且关于x=$\frac{10}{3}$对称，
则两个对称的根之和为2×$\frac{10}{3}$=$\frac{20}{3}$，
则四个根之和为2×$\frac{20}{3}$=$\frac{40}{3}$，
即m=$\frac{40}{3}$，则f（m）=f（$\frac{40}{3}$）=|lg|$\frac{40}{3}$-$\frac{10}{3}$||=|lg10|=1，
故答案为：1

点评 本题主要考查函数根的应用，利用函数的对称性是解决本题的关键．