题目内容
16．已知函数f（x）=|x|（x+m）．g（x）=|x|+|x-1|（1）若f（x）是定义域为R的奇函数，试求实数m的值
（2）在（1）的条件下，若函数h（x）=f（x）+g（x）-2a有三个零点，试求实数a的取值范围．
分析 （1）若f（x）是定义域为R的奇函数，利用f（0）=0，即可求实数m的值．
（2）利用函数和方程之间的关系将函数转化为两个图象的交点问题，利用数形结合进行求解即可．
解答 解：（1）若f（x）是定义域为R的奇函数，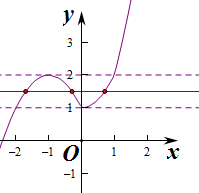
则f（0）=0，即m=0．
（2）∵函数f（x）+g（x）=2a有三个零点，
∴方程f（x）+g（x）=2a有三个解，
即x|x|+|x|+|x-1|=2a，
设$G（x）=f（x）+g（x）=\left\{\begin{array}{l}-{x^2}-2x+1（x＜0）\\{x^2}+1（0≤x＜1）\\{x^2}+2x-1（x≥1）\end{array}\right.$，
画出G（x）的图象可知：
若函数h（x）=f（x）+g（x）-2a有三个零点，
则1＜2a＜2，
解得$\frac{1}{2}$＜a＜1
故$a∈（\frac{1}{2}，1）$
点评 本题主要考查函数与方程的关系的应用，以及函数奇偶性的应用，利用函数与方程之间的关系转化为两个图象的交点问题，结合数形结合是解决本题的关键．
练习册系列答案
相关题目
6．如图所示，当输入的实数x∈[2，30]时，执行如图所示的程序框图，则输出的x不小于111的概率是（ ）
| A． | $\frac{8}{13}$ | B． | $\frac{17}{28}$ | C． | $\frac{2}{3}$ | D． | $\frac{18}{29}$ |
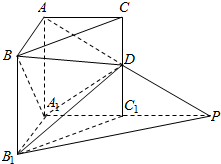如图所示，在直三棱柱ABC-A1B1B1中，∠BAC=90°，AB=AC=AA1=1，P是AD的延长线与A1C1的延长线的交点，且PB1∥平面BDA1．
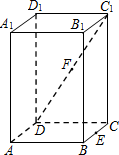如图，在正四棱柱（底面是正方形的直棱柱）ABCD-A1B1C1D1中，E是BC的中点，F是C1D的中点，P是棱CC1所在直线上的动点．则下列四个命题：
8．双曲线C的中心在原点，焦点在y轴上，离心率为$\sqrt{2}$，双曲线C与抛物线y2=4x的准线交于A，B两点，|AB|=4，则双曲线C的实轴长为（ ）
| A． | 2 | B． | $\sqrt{3}$ | C． | 4 | D． | $2\sqrt{3}$ |
5．已知全集U=R，M={x|x2＜2x}，则∁UM=（ ）
| A． | {x|X≥2} | B． | {x|x＞2} | C． | {x|x≤0或x≥2} | D． | {x|0＜x＜2} |