题目内容
7.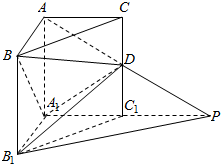 如图所示,在直三棱柱ABC-A1B1B1中,∠BAC=90°,AB=AC=AA1=1,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA1.
如图所示,在直三棱柱ABC-A1B1B1中,∠BAC=90°,AB=AC=AA1=1,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA1.(1)求证:CD=C1D.
(2)求二面角A-A1D-B的平面角的余弦值.
分析 (I)连接B1A交BA1于O,由已知条件推导出△ACD≌△PC1D,由此能够证明CD=C1D;
(II)以A1为坐标原点,以A1B1,A1C1,A1A所在直线建立空间直角坐标系,利用平面法向量与二面角的大小之间的关系求出二面角的大小.
解答  (Ⅰ)证明:连接B1A交BA1于O,
(Ⅰ)证明:连接B1A交BA1于O,
∵PB1∥平面BDA1,B1P?面AB1P,面AB1P∩面BA1D=OD,…(2分)
∴B1P∥OD,又O为B1A的中点,
∴D为AP中点,∴C1为A1P中点,…(3分)
∴△ACD≌△PC1D,∴CD=C1D.…(4分)
(Ⅱ)解:∵在直三棱柱ABC-A1B1C1中,BC=$\sqrt{2}$,AB=AC=1,
∴AB⊥AC,…(5分)
以A1为坐标原点,以A1B1,A1C1,A1A所在直线建立空间直角坐标系如图所示.
由(Ⅰ)知C1为A1P中点,
∴A1(0,0,0),B(1,0,1),D(0,1,$\frac{1}{2}$),P(0,2,0),
∴$\overrightarrow{{A}_{1}B}$=(1,0,1),$\overrightarrow{{A}_{1}D}$=(0,1,$\frac{1}{2}$),
设平面BA1D的一个法向量为$\overrightarrow{n}$=(a,b,c),则$\left\{\begin{array}{l}{a+c=0}\\{b+\frac{c}{2}=0}\end{array}\right.$,
∴$\overrightarrow{n}$=(1,$\frac{1}{2}$,-1)
又$\overrightarrow{m}$=(1,0,0)为平面AA1D的一个法向量,
∴cos<$\overrightarrow{n}$,$\overrightarrow{m}$>=$\frac{2}{3}$.
故二面角A-A1D-B的平面角的余弦值为$\frac{2}{3}$.…(12分)
点评 此题重点考查了利用空间向量的方法求点到平面的距离和二面角的大小,还考查了利用方程的思想求解坐标中所设的变量的大小.

| A. | (0,2) | B. | [0,2) | C. | (0,2] | D. | [0,2] |
| A. | 等腰直角三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
| A. | 12 | B. | 14 | C. | 6 | D. | 7 |
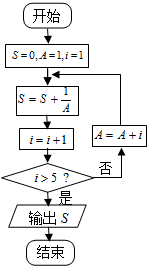
| A. | $\frac{3}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{8}{5}$ | D. | $\frac{12}{7}$ |
| A. | ${(\frac{1}{4})^a}<{(\frac{1}{3})^b}$ | B. | $\frac{1}{a}>\frac{1}{b}$ | C. | ln(a-b)>0 | D. | 3a-b<1 |
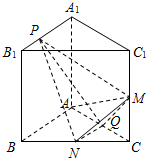 如图,已知直三棱柱ABC-A1B1C1中,AA1=AB=AC,AB⊥AC,M,N,Q分别是CC1,BC,AC的中点,点P在线段A1B1上运动.
如图,已知直三棱柱ABC-A1B1C1中,AA1=AB=AC,AB⊥AC,M,N,Q分别是CC1,BC,AC的中点,点P在线段A1B1上运动.