题目内容
7.已知点M(a,b)在直线3x+4y=15上,则$\sqrt{{a}^{2}+{b}^{2}-2a-2b+2}$的最小值为$\frac{8}{5}$.分析 由于$\sqrt{{a}^{2}+{b}^{2}-2a-2b+2}$ 表示直线3x+4y=15上点M(a,b)与点N(1,1)之间的距离,故它的最小值为点N到直线3x+4y=15的距离,再利用点到直线的距离公式求得结果.
解答 解:由题意可得3a+4b=15,则$\sqrt{{a}^{2}+{b}^{2}-2a-2b+2}$=$\sqrt{{(a-1)}^{2}{+(b-1)}^{2}}$ 表示直线3x+4y=15上点M(a,b)与点N(1,1)之间的距离,
故它的最小值为点N到直线3x+4y=15的距离,为$\frac{|3+4-15|}{\sqrt{9+16}}$=$\frac{8}{5}$,
故答案为:$\frac{8}{5}$.
点评 本题主要考查两点间的距离公式、点到直线的距离公式的应用,属于基础题.

练习册系列答案
相关题目
19.已知某几何体的三视图(单位:cm),如图所示,则此几何体的外接球的体积为( )
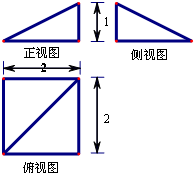

| A. | $\frac{9}{2}$πcm3 | B. | 36πcm3 | C. | $\frac{64}{3}$πcm3 | D. | 9πcm3 |
 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为平行四边形,∠ADB=90°,AB=2AD.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为平行四边形,∠ADB=90°,AB=2AD.