题目内容
15.在平面直角坐标系中,O为原点A(-1,0),B(0,$\sqrt{5}$),C(3,0),动点D满足|$\overrightarrow{CD}$|=1,则|$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OD}$|的最大值是4.分析 设D(x,y),由题意和两点之间的距离公式求出动点D的轨迹方程和轨迹,由向量的坐标运算求出$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OD}$的坐标,再判断出$|\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OD}|$的几何意义,并求出最大值.
解答 解:设D(x,y),
因为C(3,0),动点D满足|$\overrightarrow{CD}$|=1,
所以(x-3)2+y2=1,
则动点D的轨迹是以(3,0)为圆心、以1为半径的圆,
由A(-1,0),B(0,$\sqrt{5}$)得,$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OD}$=(x-1,y+$\sqrt{5}$),
则$|\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OD}|$的几何意义是点(1,-$\sqrt{5}$)到圆(x-3)2+y2=1上的点的距离,
因为点(1,-$\sqrt{5}$)在圆外,所以$|\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OD}|$的最大值是:$\sqrt{{(1-3)}^{2}+{(-\sqrt{5})}^{2}}$+1=4,
故答案为:4.
点评 本题考查了向量的坐标运算,两点之间的距离公式,动点的轨迹方程,以及代数式子的几何意义,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
10.P是直线2x-y+1=0上,且P到直线4x-3y-4=0的距离为1,则P点的坐标为( )
| A. | (-6,-11) | B. | (-1,-1) | C. | (-6,-11)或(-1,-1) | D. | (6,-11)或(-1,1) |
20.一个几何体的三视图如图所示(单位:m),则该几何体的表面积为(单位:m2)( )


| A. | (11+$4\sqrt{2}$)π | B. | (12+4$\sqrt{2}$)π | C. | (13+4$\sqrt{2}$)π | D. | (14+4$\sqrt{2}$)π |
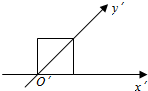 用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个边长为1的正方形,则原来的图形的面积是2$\sqrt{2}$.
用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个边长为1的正方形,则原来的图形的面积是2$\sqrt{2}$.