题目内容
19.已知函数f(x)=ex-aln(x+1)-1在点P(0,f(0))处的切线垂直于y轴.(1)求函数f(x)的单调区间;
(2)当m>n>0时,求证;em-n-1>ln(m+1)-ln(n+1)
分析 (1)求出函数的导数,求得切线的斜率,由题意可得k=f′(0)=e0-a=0,解得a=1,再由导数,解不等式即可得到单调区间;
(2)当m>n>0时,由f(x)在(0,+∞)递增,可得f(m-n)>f(0)=0,即为em-n-1>ln(1+m-n),判断ln(1+m-n)-ln(1+m)+ln(1+n)的符号,运用对数的运算性质和不等式的性质,即可得证.
解答 解:(1)函数f(x)=ex-aln(x+1)-1的导数f′(x)=ex-$\frac{a}{x+1}$,
由题意可得在点P(0,f(0))处的切线斜率为k=f′(0)=e0-a=0,
解得a=1,
即有f(x)=ex-ln(x+1)-1,f′(x)=ex-$\frac{1}{x+1}$,
由f′(x)>0,可得x>0,由f′(x)<0,可得-1<x<0,
则f(x)的单调增区间为(0,+∞),减区间为(-1,0);
(2)证明:当m>n>0时,由f(x)在(0,+∞)递增,可得
f(m-n)>f(0)=0,
即为em-n-1>ln(1+m-n),
由ln(1+m-n)-ln(1+m)+ln(1+n)=ln$\frac{(1+m-n)(1+n)}{1+m}$
=ln(1+$\frac{n(m-n)}{1+m}$)>ln1=0,
即有ln(1+m-n)>ln(1+m)-ln(1+n),
则有当m>n>0时,em-n-1>ln(m+1)-ln(n+1).
点评 本题考查导数的运用:求切线的斜率和单调区间,同时考查不等式的证明,运用函数的单调性和对数的运算性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
10.P是直线2x-y+1=0上,且P到直线4x-3y-4=0的距离为1,则P点的坐标为( )
| A. | (-6,-11) | B. | (-1,-1) | C. | (-6,-11)或(-1,-1) | D. | (6,-11)或(-1,1) |
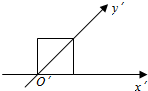 用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个边长为1的正方形,则原来的图形的面积是2$\sqrt{2}$.
用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个边长为1的正方形,则原来的图形的面积是2$\sqrt{2}$. 如图,C是圆O的直径AB上一点,CD⊥AB,与圆O相交于点D,与弦AF交于点E,与BF的延长线相交于点G.GT与圆相切于点T.
如图,C是圆O的直径AB上一点,CD⊥AB,与圆O相交于点D,与弦AF交于点E,与BF的延长线相交于点G.GT与圆相切于点T.