题目内容
16.设函数f(x)=$\frac{ex}{{e}^{x}}$的导数为f'(x)(e为自然对数的底数).(1)求函数f(x)的极大值;
(2)解方程f(f(x))=x;
(3)若存在实数x1,x2(x1≠x2)使得f(x1)=f(x2),求证:f($\frac{{x}_{1}+{x}_{2}}{2}$)<0.
分析 (1)对f(x)求导,f'(x)=0求出极值点,根据单调性求出极大值
(2)构造新函数,利用新函数的导数说明单调性,继而说明方程根的个数.
(3)由题意,f(x1)=f(x2),则$\frac{e{x}_{1}}{{e}^{{x}_{1}}}=\frac{e{x}_{2}}{{e}^{{x}_{2}}}$,不妨设0<x1<x2,构造函数,利用函数单调性证明.
解答 解:(1)函数f(x)得定义域为R,f'(x)=e$\frac{(1-x)}{{e}^{x}}$
当$x∈(-∞,1)\\;\\;\\;时,f'(x)>0$,时,f'(x)>0,f(x)单调递增
当x∈(1,+∞)时,f'(x)<0,f(x)单调递减
则f(x)max=f(1)=1.
(2)f(f(x))=$\frac{ef(x)}{{e}^{f(x)}}=\frac{e\frac{ex}{{e}^{x}}}{e\frac{ex}{{e}^{x}}}=x$,若x=0,显然满足上式.若x≠0,方程等价于${e}^{2-x}={e}^{\frac{ex}{{e}^{x}}}$
故(x-2)ex+ex=0,显然当x<0时,(x-2)ex+ex<0
令g(x)=(x-2)ex+ex(x>0)g'(x)=(x-1)ex+e
g'(x)>0恒成立,故当x>0时原方程由唯一根x=1.
综上,原方程得解为x=0或x=1
(3)由题意,f(x1)=f(x2),则$\frac{e{x}_{1}}{{e}^{{x}_{1}}}=\frac{e{x}_{2}}{{e}^{{x}_{2}}}$,不妨设0<x1<x2,则${x}_{1}{e}^{{x}_{2}}={x}_{2}{e}^{{x}_{1}}$,则x1+lnx2=x2+lnx1,即$\frac{{x}_{2}-{x}_{1}}{ln{x}_{2}-ln{x}_{1}}=1$
f'(x)=e$\frac{(1-x)}{{e}^{x}}$,欲证f'($\frac{{x}_{1}+{x}_{2}}{2}$)<0,只需证$\frac{{x}_{1}+{x}_{2}}{2}>1$
只需证:$\frac{{x}_{2}-{x}_{1}}{ln{x}_{2}-ln{x}_{1}}<\frac{{x}_{1}+{x}_{2}}{2}$,只需证:$\frac{{x}_{2}-{x}_{1}}{{x}_{1}+{x}_{2}}<\frac{ln{x}_{2}-ln{x}_{1}}{2}$
只需证:$\frac{\frac{{x}_{2}}{{x}_{1}}-1}{\frac{{x}_{2}}{{x}_{1}}+1}<\frac{ln\frac{{x}_{2}}{{x}_{1}}}{2}$,令t=$\frac{{x}_{2}}{{x}_{1}}$,h(t)=$\frac{t-1}{t+1}-\frac{1}{2}lnt,t∈(1,+∞)$
h'(t)=$\frac{2}{(t+1)^{2}}-\frac{1}{2t}=\frac{-(t-1)^{2}}{2t(t+1)^{2}}<0$,当t∈(1,+∞)恒成立.故h(t)在t∈(1,+∞)单调递减,故h(t)<h(1)=0,所以原命题成立.
点评 本题主要考查了函数导数在求极值中得应用和证明题中得应用,属于难度较大的题型,高考经常涉及.

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案| A. | 12π | B. | 24π | C. | 144π | D. | 48π |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
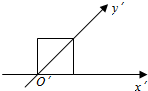 用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个边长为1的正方形,则原来的图形的面积是2$\sqrt{2}$.
用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个边长为1的正方形,则原来的图形的面积是2$\sqrt{2}$. 如图,C是圆O的直径AB上一点,CD⊥AB,与圆O相交于点D,与弦AF交于点E,与BF的延长线相交于点G.GT与圆相切于点T.
如图,C是圆O的直径AB上一点,CD⊥AB,与圆O相交于点D,与弦AF交于点E,与BF的延长线相交于点G.GT与圆相切于点T.