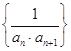题目内容
【题目】定义域为![]() 的单调函数
的单调函数![]() 满足
满足![]()
![]() ,且
,且![]() ,
,
(1)求![]() ,
,![]() ;
;
(2)判断函数![]() 的奇偶性,并证明;
的奇偶性,并证明;
(3)若对于任意![]() 都有
都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)奇函数;(3)
;(2)奇函数;(3)![]()
【解析】
(1)取![]() 代入函数满足的等式,整理可得
代入函数满足的等式,整理可得![]() .再根据
.再根据![]() ,结合定义和
,结合定义和![]() ,算出
,算出![]() ;
;
(2)以![]() 取代
取代![]() ,代入函数满足的等式,可得
,代入函数满足的等式,可得![]() ,由此可得
,由此可得![]() 是奇函数;
是奇函数;
(3)根据函数是单调函数且![]() ,得
,得![]() 是定义域在
是定义域在![]() 上的增函数.再结合函数为奇函数,将题中不等式转化为
上的增函数.再结合函数为奇函数,将题中不等式转化为![]() 在
在![]() 上恒成立,最后采用变量分离的方法结合换元法求函数的最大值,可算出
上恒成立,最后采用变量分离的方法结合换元法求函数的最大值,可算出![]() 的取值范围.
的取值范围.
解:(1)取![]() ,得
,得![]() ,
,
即![]() ,
,![]() ,
,
![]()
![]() 结合
结合![]() ,得
,得![]() ,可得
,可得![]() ;
;
(2)取![]() ,得
,得![]()
移项得![]()
![]() 函数
函数![]() 是奇函数;
是奇函数;
(3)![]() 是奇函数,且
是奇函数,且![]() 在
在![]() 上恒成立,
上恒成立,
![]() 在
在![]() 上恒成立,
上恒成立,
又![]() 是定义域在
是定义域在![]() 的单调函数,且
的单调函数,且![]() ,
,
![]() 是定义域在
是定义域在![]() 上的增函数.
上的增函数.
![]() 在
在![]() 上恒成立.
上恒成立.
![]()
![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,
,
由于![]() ,
,![]()
![]() .
.
![]() .
.![]() .
.
则实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某电视台为宣传本省,随机对本省内15~65岁的人群抽取了![]() 人,回答问题“本省内著名旅游景点有哪些”统计结果如图表所示.
人,回答问题“本省内著名旅游景点有哪些”统计结果如图表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 |
|
|
|
第2组 |
| 18 |
|
第3组 |
|
|
|
第4组 |
|
|
|
第5组 |
|
|
|

(1)分别求出![]() 的值;
的值;
(2)从第2、3、4组回答正确的人中用分层抽样的方法抽取6人,求第2、3、4组每组各抽取多少人?
(3)指出直方图中,这组数据的中位数是多少(取整数值)?