题目内容
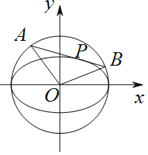
【题目】已知直线l:y=kx+m与椭圆![]() +
+![]() =1(a>b>0)恰有一个公共点P,l与圆x2+y2=a2相交于A,B两点.
=1(a>b>0)恰有一个公共点P,l与圆x2+y2=a2相交于A,B两点.
(Ⅰ)求m(用a,b,k表示);
(Ⅱ)当k=-![]() 时,△AOB的面积的最大值为
时,△AOB的面积的最大值为![]() a2,求椭圆的离心率.
a2,求椭圆的离心率.
【答案】(Ⅰ)m=±![]() ; (Ⅱ)
; (Ⅱ)![]()
【解析】
(Ⅰ)根据题意,联立直线与椭圆的方程,变形可得(a2k2+b2)x2+2a2kmx+a2(m2-b2)=0,由直线与椭圆的位置关系可得△=(2a2km)2-4(a2k2+b2)a2(m2-b2)=0,整理变形可得答案;
(Ⅱ)根据题意,求出原点O到直线l的距离,变形可得![]() ,结合椭圆的离心率公式分析可得答案.
,结合椭圆的离心率公式分析可得答案.
解:(Ⅰ)根据题意,直线l与椭圆![]() 恰有一个公共点P,即相切;
恰有一个公共点P,即相切;
则有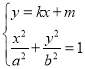 ,得(a2k2+b2)x2+2a2kmx+a2(m2-b2)=0,
,得(a2k2+b2)x2+2a2kmx+a2(m2-b2)=0,
则△=(2a2km)2-4(a2k2+b2)a2(m2-b2)=0,
化简整理,得m2=a2k2+b2;m=±![]() ,
,
(Ⅱ)因为当![]() 时,△OAB的面积取到最大值
时,△OAB的面积取到最大值![]() ,
,
此时OA⊥OB,从而原点O到直线l的距离![]() ,
,
又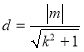 ,故
,故![]() ;
;
再由(I),得![]() ,则
,则![]() .
.
又![]() ,故
,故![]() ,即
,即![]() ,
,
从而![]() ,即
,即![]() .
.

练习册系列答案
相关题目