题目内容
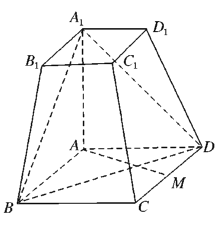
【题目】如图,正方体![]() 的棱长为a,
的棱长为a,![]() 分别是棱
分别是棱![]() 、
、![]() 的中点,过点
的中点,过点![]() 的平面分别与棱
的平面分别与棱![]() 、
、![]() 交于点
交于点![]() ,设
,设![]() ,
,![]() ,给出以下四个命题:
,给出以下四个命题:
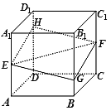
(1)平面![]() 与平面
与平面![]() 所成角的最大值为
所成角的最大值为![]() ;
;
(2)四边形![]() 的面积的最小值为
的面积的最小值为![]() ;
;
(3)四棱锥![]() 的体积为
的体积为![]() ;
;
(4)点![]() 到平面
到平面![]() 的距离的最大值为
的距离的最大值为![]() ,
,
其中正确的个数为( )
A.1B.2C.3D.4
【答案】C
【解析】
由两平面所成角的余弦公式即面积射影公式,计算可得所求最大值,可判断(1);
由四边形![]() 为菱形,计算面积,考虑
为菱形,计算面积,考虑![]() 的最小值,可判断(2);
的最小值,可判断(2);
由棱锥的等体积法,计算可判断(3);
由等体积法和函数的性质可判断(4);
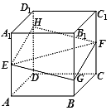
对于(1),由面面平行的性质定理可得![]() ,可得四边形
,可得四边形![]() 为平行四边形,又直角梯形
为平行四边形,又直角梯形![]() 和直角梯形
和直角梯形![]() 全等,可得
全等,可得![]() ,即有四边形
,即有四边形![]() 为菱形,且
为菱形,且![]() ,由平面
,由平面![]() 在底面上的射影为四边形
在底面上的射影为四边形![]() ,
,
由面积射影公式可得
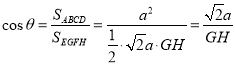
由![]() ,可得
,可得![]() ,可得平面
,可得平面![]() 与平面
与平面![]() 所成角的最大值不为
所成角的最大值不为![]() ,故(1)错;
,故(1)错;
对于(2),由![]() ,可得菱形
,可得菱形![]() 的面积的最小值为
的面积的最小值为![]()
故(2)正确;
对于(3),因为四棱锥![]() 的体积为
的体积为
![]() ,故(3)正确;
,故(3)正确;
对于(4)![]()
![]()
设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,可得
,可得
![]() ,
,
可得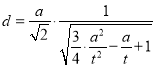 ,(其中
,(其中![]() ),当
),当![]() 即
即![]() 时,
时,
![]() 取得最大值
取得最大值![]() ,故(4)正确;
,故(4)正确;
故选:C

练习册系列答案
相关题目