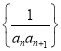题目内容
【题目】古希腊数学家阿波罗尼奧斯（约公元前262～公元前190年）的著作《圆锥曲线论》是古代世界光辉的科学成果，他证明过这样一个命题：平面内与两定点距离的比为常数k（k＞0，k≠1）的点的轨迹是圆，后人将这个圆称为阿波罗尼斯圆．在平面直角坐标系中，设A（﹣3，0），B（3，0），动点M满足
＝2，则动点M的轨迹方程为（）
A. （x﹣5）2+y2＝16B. x2+（y﹣5）2＝9
C. （x+5）2+y2＝16D. x2+（y+5）2＝9
【答案】A
【解析】
首先设
，代入两点间的距离求
和
，最后整理方程.
解析：设，由
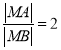，得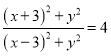
，
可得：（x+3）2+y2＝4（x﹣3）2+4y2，
即x2﹣10x+y2+9＝0
整理得
，故动点
的轨迹方程为.选A.
练习册系列答案
发散思维新课堂系列答案
相关题目
