题目内容
根据下列条件求椭圆的标准方程:
(1)已知P点在以坐标轴为对称轴的椭圆上,点P到两焦点的距离分别为 和
和 ,过P作长轴的垂线恰好过椭圆的一个焦点;
,过P作长轴的垂线恰好过椭圆的一个焦点;
(2)经过两点A(0,2)和B .
.
(1)已知P点在以坐标轴为对称轴的椭圆上,点P到两焦点的距离分别为
 和
和 ,过P作长轴的垂线恰好过椭圆的一个焦点;
,过P作长轴的垂线恰好过椭圆的一个焦点;(2)经过两点A(0,2)和B
 .
.(1)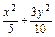 =1或
=1或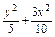 =1(2)
=1(2)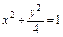
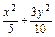 =1或
=1或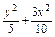 =1(2)
=1(2)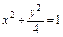
(1)设椭圆的标准方程是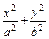 =1或
=1或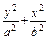 =1,
=1,
则由题意知2a=|PF1|+|PF2|=2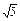 ,∴a=
,∴a=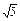 .
.
在方程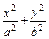 =1中令x=±c得|y|=
=1中令x=±c得|y|=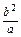
在方程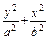 =1中令y=±c得|x|=
=1中令y=±c得|x|=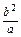
依题意并结合图形知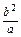 =
= . ∴b2=
. ∴b2=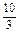 .
.
即椭圆的标准方程为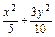 =1或
=1或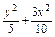 =1.
=1.
(2)设经过两点A(0,2),B 的椭圆标准方程为
的椭圆标准方程为
mx2+ny2=1,代入A、B得
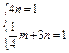
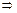
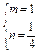 , ∴所求椭圆方程为
, ∴所求椭圆方程为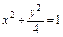 .
.
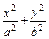 =1或
=1或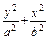 =1,
=1,则由题意知2a=|PF1|+|PF2|=2
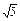 ,∴a=
,∴a=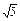 .
.在方程
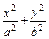 =1中令x=±c得|y|=
=1中令x=±c得|y|=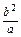
在方程
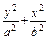 =1中令y=±c得|x|=
=1中令y=±c得|x|=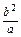
依题意并结合图形知
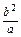 =
= . ∴b2=
. ∴b2=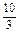 .
.即椭圆的标准方程为
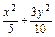 =1或
=1或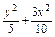 =1.
=1.(2)设经过两点A(0,2),B
 的椭圆标准方程为
的椭圆标准方程为mx2+ny2=1,代入A、B得
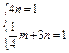
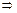
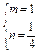 , ∴所求椭圆方程为
, ∴所求椭圆方程为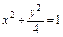 .
.
练习册系列答案
相关题目
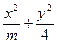 =1的焦距为2,则m的值等于__________________.
=1的焦距为2,则m的值等于__________________. 的椭圆
的椭圆 过点
过点 ,
, 是坐标原点.
是坐标原点. 的方程;
的方程; 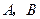 为椭圆
为椭圆 ,判定直线
,判定直线 与圆
与圆 的位置关系,并证明你的结论.
的位置关系,并证明你的结论. 是椭圆
是椭圆 的左、右焦点,
的左、右焦点, 是椭圆上位于第一象限内的一点,点
是椭圆上位于第一象限内的一点,点 也在椭圆上,且满足
也在椭圆上,且满足 (
( 为坐标原点),
为坐标原点), .若椭圆的离心率等于
.若椭圆的离心率等于 .
. 的方程;
的方程; 的面积等于
的面积等于 ,求椭圆的方程.
,求椭圆的方程. 中,已知
中,已知 ,且当顶点
,且当顶点 位于定点
位于定点 时,
时, 有最小值为
有最小值为 .(1)建立适当的坐标系,求顶点
.(1)建立适当的坐标系,求顶点 作直线与(1)中的曲线交于
作直线与(1)中的曲线交于 、
、 两点,求
两点,求 的最小值的集合.
的最小值的集合. ,一个焦点是F(-m,0)(m是大于0的常数).
,一个焦点是F(-m,0)(m是大于0的常数). |=2|
|=2| |,求直线l的斜率.
|,求直线l的斜率. 左右焦点分别为
左右焦点分别为 、
、 ,点
,点 在椭圆上,若
在椭圆上,若 轴的距离为( )
轴的距离为( ) B 3 C
B 3 C  D
D 





 交椭圆
交椭圆 于
于 两点,椭圆与
两点,椭圆与 轴的正半轴交于
轴的正半轴交于 点,若
点,若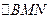 的重心恰好落在椭圆的右焦点,则直线
的重心恰好落在椭圆的右焦点,则直线


