题目内容
【题目】已知集合A={x|﹣2≤x≤5}，B={x|m﹣4≤x≤3m+3}．
（1）若AB，求实数m的取值范围；
（2）若A∩B=B，求实数m的取值范围．
【答案】
（1）解：∵集合A={x|﹣2≤x≤5}，B={x|m﹣4≤x≤3m+3}．
AB，
∴ 
，
解得1≤m≤2．
∴实数m的取值范围是[1，2]
（2）解：∵A∩B=B，∴BA，
①当B=时，贼》3m+2，∴m＜﹣3符合题意；
②当B≠时，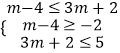 
，无解．
综上可得，m＜﹣3．
∴实数m的取值范围是（﹣∞，﹣3）
【解析】（1）由AB，列出不等式组，即可求解实数m的取值范围．（2）由A∩B=B，根据B=和B≠分类讨论，分别求解实数m的取值范围，取并集即可求解m的取值范围．
【考点精析】利用集合的交集运算对题目进行判断即可得到答案，需要熟知交集的性质：（1）A∩B
A，A∩BB，A∩A=A，A∩
=,A∩B=B∩A;（2）若A∩B=A，则AB，反之也成立．
练习册系列答案
相关题目
