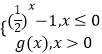��Ŀ����
����Ŀ����֪������[1��+�ޣ��ϵĺ���f��x��=  �������н��ۣ�
�������н��ۣ�
�ٺ���f��x����ֵ��Ϊ��0��8]��
�ڶ������n��N������f��2n��=23��n��
�۴���k�ʣ� ![]() ��
�� ![]() ����ʹ��ֱ��y=kx�뺯��y=f��x����ͼ����5�������㣻
����ʹ��ֱ��y=kx�뺯��y=f��x����ͼ����5�������㣻
�ܡ�����f��x�������䣨a��b���ϵ����ݼ����ij�Ҫ�����ǡ�����n��N��ʹ�ã�a��b����2n �� 2n+1����
������ȷ���������ǣ� ��
A.�٢ڢ�
B.�٢ۢ�
C.�٢ڢ�
D.�ڢۢ�
���𰸡�C
���������⣺�ٵ�1��x��2ʱ��f��x��=��8x��x��2��=��8��x��1��2+8�ʣ�0��8]��
�ڡ�f��1��=8����f��2n��= ![]() f��2n��1��=
f��2n��1��= ![]() f��2n��2��=
f��2n��2��= ![]() f��2n��3��=��=
f��2n��3��=��= ![]() f��20��=
f��20��= ![]() f��1��=
f��1��= ![]() ��8=23��n �� �ʢ���ȷ���۵�x��2ʱ��f��x��=
��8=23��n �� �ʢ���ȷ���۵�x��2ʱ��f��x��= ![]() f��
f�� ![]() ����0��4]���ʺ���f��x����ֵ��Ϊ��0��8]���ʢ���ȷ����2��x��4ʱ��1��
����0��4]���ʺ���f��x����ֵ��Ϊ��0��8]���ʢ���ȷ����2��x��4ʱ��1�� ![]() ��2����f��x��=
��2����f��x��= ![]() f��
f�� ![]() ��=
��= ![]() [��8��
[��8�� ![]() ��1��2+8]=��4��
��1��2+8]=��4�� ![]() ��1��2+4����4��x��8ʱ��2��
��1��2+4����4��x��8ʱ��2�� ![]() ��4����f��x��=
��4����f��x��= ![]() f��
f�� ![]() ��=
��= ![]() [��4��
[��4�� ![]() ��1��2+4]=��2��
��1��2+4]=��2�� ![]() ��1��2+2����������f��x����ͼ����ͼ������y=
��1��2+2����������f��x����ͼ����ͼ������y= ![]() x��y=
x��y= ![]() x��ͼ����ͼ����k�ʣ�
x��ͼ����ͼ����k�ʣ� ![]() ��
�� ![]() ����ʹ��ֱ��y=kx�뺯��y=f��x����ͼ����3�������㣻�ʢ۴����ɷֶκ����ı���ʽ�õ�x�ʣ�2n �� 2n+1��ʱ������f��x���ڣ�2n �� 2n+1����Ϊ�����ݼ�����������f��x�������䣨a��b���ϵ����ݼ����ij�Ҫ�����ǡ�����n��N��ʹ�ã�a��b��
����ʹ��ֱ��y=kx�뺯��y=f��x����ͼ����3�������㣻�ʢ۴����ɷֶκ����ı���ʽ�õ�x�ʣ�2n �� 2n+1��ʱ������f��x���ڣ�2n �� 2n+1����Ϊ�����ݼ�����������f��x�������䣨a��b���ϵ����ݼ����ij�Ҫ�����ǡ�����n��N��ʹ�ã�a��b��
�����㾫�������ڱ��⿼������������ж���Ӧ�ã���Ҫ�˽��������⻥Ϊ������⣬��������ͬ������ԣ���������Ϊ������������⣬���ǵ������û�й�ϵ���ܵó���ȷ�𰸣�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�