题目内容
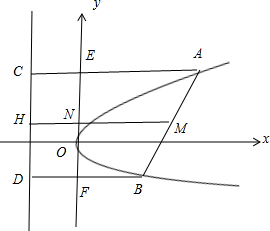
长度为a的线段AB的两个端点A、B都在抛物线y2=2px(p>0,a>2p)上滑动,则线段AB的中点M到y轴的最短距离为______.
由题意可得抛物线的准线l:x=-
分别过A,B,M作AC⊥l,BD⊥l,MH⊥l,垂足分别为C,D,H
在直角梯形ABDC中MH=
由抛物线的定义可知AC=AF,BD=BF(F为抛物线的焦点)
MH=
≥
=
即AB的中点M到抛物线的准线的最小距离为
∴线段 AB的中点M到y轴的最短距离为
(a-p)
故答案为
(a-p)
| p |
| 2 |
分别过A,B,M作AC⊥l,BD⊥l,MH⊥l,垂足分别为C,D,H
在直角梯形ABDC中MH=
| AC+BD |
| 2 |
由抛物线的定义可知AC=AF,BD=BF(F为抛物线的焦点)
MH=
| AF+BF |
| 2 |
| AB |
| 2 |
| a |
| 2 |
即AB的中点M到抛物线的准线的最小距离为
| a |
| 2 |
∴线段 AB的中点M到y轴的最短距离为
| 1 |
| 2 |
故答案为
| 1 |
| 2 |


练习册系列答案
相关题目
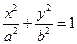
 的中心.椭圆的离心率是抛物线离心率的一半,且它们的准线互相平行。又抛物线与椭圆交于点
的中心.椭圆的离心率是抛物线离心率的一半,且它们的准线互相平行。又抛物线与椭圆交于点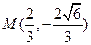 ,求抛物线与椭圆的方程.
,求抛物线与椭圆的方程.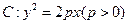 上任意一点到焦点F的距离比到
上任意一点到焦点F的距离比到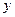 轴的距离大1,(1)求抛物线C的方程;(2)若过焦点F的直线交抛物线于M,N两点,M在第一象限,且
轴的距离大1,(1)求抛物线C的方程;(2)若过焦点F的直线交抛物线于M,N两点,M在第一象限,且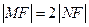 ,求直线MN的方程;(3)过点
,求直线MN的方程;(3)过点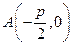 的直线交抛物线
的直线交抛物线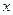 轴的对称点为R,求证:直线RQ必过定点.
轴的对称点为R,求证:直线RQ必过定点.