题目内容
14.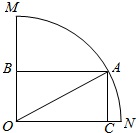 如图:已知扇形MON所在圆半径为1,∠MON=$\frac{π}{2}$,扇形内接矩形ABOC,设∠AON=θ.
如图:已知扇形MON所在圆半径为1,∠MON=$\frac{π}{2}$,扇形内接矩形ABOC,设∠AON=θ.(1)将矩形面积S表示为θ的函数,并指出θ的取值范围;
(2)当θ取何值时,矩形面积S最大,并求S的最大值.
分析 (1)由图形得到矩形的长宽,得到矩形的面积;
(2)利用(1)的结论集合正弦函数的有界性求最大值.
解答 解:(1)由条件OA=1,∠AON=θ.
∴OC=cosθ,AC=sinθ…2分
∴S=sinθcosθ=$\frac{1}{2}$sin2θ …4分
其中0<$θ<\frac{π}{2}$ …6分
(2)∵$0<θ<\frac{π}{2}$,∴0<2θ<π…8分
故当$2θ=\frac{π}{2}$,即$θ=\frac{π}{4}$时,…10分
${S}_{max}=\frac{1}{2}$.…12分.
点评 本题考查了三角函数的应用;用到了正弦函数的有界性;比较基础.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
5.已知随机变量x服从二项分布x~B(6,$\frac{1}{3}$),则P(x=2)等于( )
| A. | $\frac{80}{243}$ | B. | $\frac{4}{243}$ | C. | $\frac{13}{243}$ | D. | $\frac{13}{16}$ |
2.当输入x=-1,y=20时,如图中程序运行后输出的结果为 ( )


| A. | 3; 43 | B. | 43;3 | C. | -18;16 | D. | 16;-18 |
19.否定“自然数m,n,k中恰有一个奇数”时正确的反设为( )
| A. | m,n,k都是奇数 | B. | m,n,k都是偶数 | ||
| C. | m,n,k中至少有两个偶数 | D. | m,n,k都是偶数或至少有两个奇数 |