题目内容
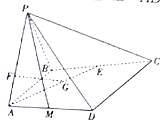
【题目】如下图,已知椭圆![]() 的上顶点为
的上顶点为![]() ,左、右顶点为
,左、右顶点为![]() ,右焦点为
,右焦点为![]() ,
, ![]() ,且
,且![]() 的周长为14.
的周长为14.
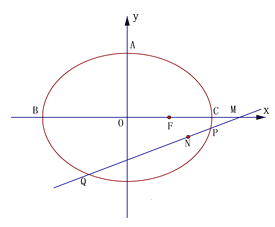
(I)求椭圆的离心率;
(II)过点![]() 的直线
的直线![]() 与椭圆相交于不同两点
与椭圆相交于不同两点![]() ,点N在线段
,点N在线段![]() 上.设
上.设![]() ,试判断点
,试判断点![]() 是否在一条定直线上,并求实数λ的取值范围.
是否在一条定直线上,并求实数λ的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)根据条件计算得![]() 的值,进而可求离心率;
的值,进而可求离心率;
(Ⅱ)设l的方程为![]() ,与椭圆联立得
,与椭圆联立得![]() ,
, ![]() ,根据条件
,根据条件![]() ,化简得
,化简得![]() ,带入条件可得
,带入条件可得![]() ,由
,由![]() 即可求得
即可求得![]() 的范围.
的范围.
试题解析:
(I)由![]() ,得
,得![]() ,
,
![]() 的周长为
的周长为![]() ,即
,即![]() ,得
,得![]() ,
,
所以![]() ,椭圆的离心率为
,椭圆的离心率为![]() ;
;
(II)显然直线l的斜率存在,设l的方程为![]() ,
,
设P(x1,y1),Q(x2,y2),N(x0,y0),
由![]() ,得
,得![]() ,化简得
,化简得![]() ①,-----6分
①,-----6分
由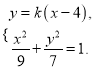 消去x,得
消去x,得![]() ,
,
得![]() ,
, ![]() ,
,
代入①式得![]() ,由
,由![]() 得
得![]() ,
,
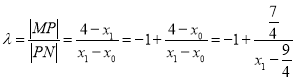 ,
,
因为![]() ,得
,得![]() ,所以
,所以![]() ,
,
因此,N在一条直线![]() 上,实数
上,实数![]() .
.
【法二:显然直线l的斜率存在,设l的方程为![]() ,不妨设
,不妨设![]() ,
,
设P(x1,y1),Q(x2,y2),N(x0,y0), ![]() ,
,
由![]() ,得
,得![]() ,化简得
,化简得![]() ①,6分
①,6分
由![]() ,
, ![]() ,得
,得![]() ②,
②,
由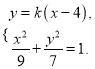 消去x,得
消去x,得![]() ,
,
可知![]()
![]()
![]() ,
,
得![]() ,
, ![]() ,
, 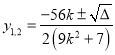 ,
,
代入①式得![]() ,由
,由![]() 得
得![]() ,
,
由②式得![]()
![]() ,得
,得![]() ,
,
因此,N在一条直线![]() 上,实数
上,实数![]() .
.
法三:设P(x1,y1),Q(x2,y2),N(x0,y0), ![]() ,由
,由![]() ,
,
得![]()
所以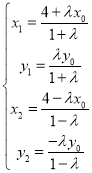 ,将
,将![]() ,
, ![]() 代入椭圆方程得
代入椭圆方程得
![]()
上面两式相减化简得![]()
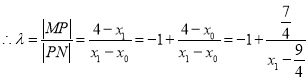 ,
,
因为![]() ,得
,得![]() ,所以
,所以![]() ,
,
因此,N在一条直线![]() 上,实数
上,实数![]() .
.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目