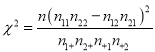题目内容
【题目】已知函数![]() 的定义域为
的定义域为![]() ,对于任意的
,对于任意的![]() 都有
都有![]() ,设
,设![]() 时,
时, ![]() .
.
(1)求![]() ;
;
(2)证明:对于任意的![]() ,
, ![]() ;
;
(3)当![]() 时,若不等式
时,若不等式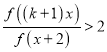 在
在![]() 上恒定成立,求实数
上恒定成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ; (2)详见解析;(3)
; (2)详见解析;(3) ![]() .
.
【解析】试题分析:(1)令![]() ,
, ![]() ,
, ![]() ;(2)令
;(2)令![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,结合
,结合![]() 时,
时, ![]() 即可得结果;(3)先证明函数
即可得结果;(3)先证明函数![]() 在
在![]() 单调递减,根据
单调递减,根据![]() ,将原不等式化为
,将原不等式化为![]() ,可得
,可得![]() 化简,利用不等式恒成立可得结果..
化简,利用不等式恒成立可得结果..
试题解析:(1)令![]() ,
, ![]() ,
, ![]()
![]() .
.
(2)由题意当![]() 时,
时, ![]()
由(1)知,当![]() ,
, ![]()
所以下证,当![]() 时,
时, ![]()
![]()
![]() ,
, ![]()
![]() .
.
(3)![]()
![]()
令![]() ,
, ![]() ,
, ![]() ,假设
,假设![]() ,
, ![]()
![]()
![]()
故函数![]() 在
在![]() 单调递减,
单调递减,
![]() 化简得:
化简得: ![]()
![]() ,
, ![]() .
.
【方法点晴】本题主要考查抽象函数的定义域、抽象函数的单调性及抽象函数解不等式,属于难题.根据抽象函数的单调性解不等式应注意以下三点:(1)一定注意抽象函数的定义域(这一点是同学们容易疏忽的地方,不能掉以轻心);(2)注意应用函数的奇偶性(往往需要先证明是奇函数还是偶函数);(3)化成![]() 后再利用单调性和定义域列不等式组.
后再利用单调性和定义域列不等式组.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】(本小题满分12分)某班主任对全班50名学生学习积极性和参加社团活动情况进行调查,统计数据如表1所示
表1
参加社团活动 | 不参加社团活动 | 合计 | |
学习积极性高 | 17 | 8 | 25 |
学习积极性一般 | 5 | 20 | 25 |
合计 | 22 | 28 | 50 |
(1)如果随机从该班抽查一名学生,抽到参加社团活动的学生的概率是多少?抽到不参加社团活动且学习积极性一般的学生的概率是多少?
(2)运用独立检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |