题目内容

11．已知函数f（x）=（x2+ax+a）ex（a≤2，x∈R）
（1）若a=1，求y=f（x）在点（0，f（0））处的切线方程；
（2）是否存在实数a，使得f（x）的极大值为3，若存在，求出a的值；若不存在，说明理由．

分析 （1）求函数的导数，利用导数的几何意义即可求y=f（x）在点（0，f（0））处的切线方程；
（2）求函数的导数，根据函数的极值和导数的关系求出函数的极大值，进行判断．

解答 解：函数的导数f′（x）=（2x+a）ex+（x2+ax+a）ex=[x2+（a+2）x+2a]ex
（1）若a=1，则f′（x）=（x2+3x+2）ex，
则f′（0）=2，f（0）=1，
即y=f（x）在点（0，f（0））处的切线方程为y-1=2x，即y=2x+1；
（2）由f′（x）=[x2+（a+2）x+2a]ex=0得x2+（a+2）x+2a=0，解得x=-2或x=-a，
当a=2时，f′（x）=（x+2）2ex＞0，此时函数单调递增，故无极值，
当a＜2时，

 x （-∞，-2）-2 （-2，-a） -a （-a，+∞） 
 f′（x）+ 0-0 +
 f（x） 递增 极大 递减 极小 递增
则当x=-2时，函数取得极大值f（-2），
由f（-2）=3得a=4-3e2．
故存在a=4-3e2．

点评 本题主要考查导数的几何意义，以及函数极值的求解，求函数的导数，利用导数进行研究是解决本题的关键．

练习册系列答案
相关题目
4．已知函数f（x）=log22x-mlog2x+a，g（x）=x2+1．
（1）当a=1时，求f（x）在x∈[1，4]上的最小值；
（2）当a＞0，m=2时，若对任意的实数t∈[1，4]，均存在xi∈[1，8]（i=1，2），且x1≠x2，使得$\frac{g（{x}_{i}-a）+2a}{{x}_{i}}$=f（t）成立，求实数a的取值范围．
5．函数f（x）是定义在实数集R上的不恒为零的偶函数，f（-1）=1，且对任意实数x都有xf（x+1）=（x+1）f（x），则f（0）+f（1）+f（2）+…+f（2015）的值是2031120．
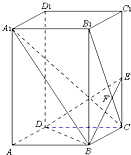2．如图，已知正四棱柱ABCD-A1B1C1D1中，底面边长AB=2，侧棱BB1的长为4，过点B作B1C的垂线交侧棱CC1于点E，交B1C于点F．
（1）求证：A1C⊥平面BDE；
（2）求三棱锥C-BDE的体积．
6．已知圆C：x2+y2-x-y=0经过椭圆E：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的右焦点F和上顶点D．
（Ⅰ）求椭圆E的方程；
（Ⅱ）过点P（-2，0）作斜率不为零的直线l与椭圆E交于不同的两点A，B，直线AF，BF分别交椭圆E于点G，H，设$\overrightarrow{AF}$=λ1$\overrightarrow{FG}$，$\overrightarrow{BF}$=λ2$\overrightarrow{FH}$．（λ1，λ2∈R）
（i）求λ1+λ2的取值范围；
（ii）是否存在直线l，使得|AF|•|GF|=|BF|•|HF|成立？若存在，求l的方程；若不存在，请说明理由．
16．某几何体的三视图如图所示，则该几何体的表面积是（　　）
A．16+8$\sqrt{3}$B．16+4$\sqrt{3}$C．48+8$\sqrt{3}$D．48+4$\sqrt{3}$
3．已知数列{an}的前n项和Sn=$\frac{1}{2}{a_n}{a_{n+1}}（n∈{N^*}）$，其中a1=1，an≠0．
（Ⅰ）求a2，a3，a4；
（Ⅱ）求数列{an}的前n个偶数项的和Tn．
20．定义[x]表示不超过x的最大整数，如[0.5]=0，[-2.5]=-3，若f（x）=cos（x-[x]），给出下列结论：
①y=f（x）为偶函数；
②y=f（x）为周期函数且周期为1；
③当x∈[0，1），f（x）是单调递增函数；
④y=f（x）的最大值是1，最小值是cos1；
⑤y=f（x）的最大值是1，无最小值．
其中正确结论的序号是②⑤．
1．已知公差不为0的等差数列{an}满足a1，a3，a4成等比数列，Sn为数列{an}的前n项和，则$\frac{{S}_{3}-{S}_{2}}{{S}_{5}-{S}_{3}}$的值为（　　）
A．2B．3C．-2D．-3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网