题目内容
20.定义[x]表示不超过x的最大整数,如[0.5]=0,[-2.5]=-3,若f(x)=cos(x-[x]),给出下列结论:①y=f(x)为偶函数;
②y=f(x)为周期函数且周期为1;
③当x∈[0,1),f(x)是单调递增函数;
④y=f(x)的最大值是1,最小值是cos1;
⑤y=f(x)的最大值是1,无最小值.
其中正确结论的序号是②⑤.
分析 作函数f(x)=cos(x-[x])的图象,则图象得到性质.
解答 解:作函数f(x)=cos(x-[x])的图象如下,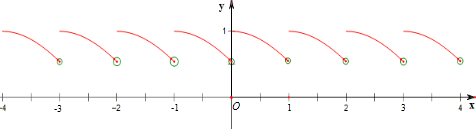
①y=f(x)不是偶函数,故不正确;
②y=f(x)为周期函数,周期为1,故正确;
③当x∈[0,1),f(x)是单调递减函数,故不正确;
④y=f(x)的最小值不存在,最大值为1,故不正确;
⑤y=f(x)无最小值,最大值为1,故正确.
故正确结论的序号是②⑤,
故答案为:②⑤
点评 本题考查了函数的图象的应用,属于基础题.

练习册系列答案
相关题目
8.已知数列{an}共有9项,其中,a1=a9=1,且对每个i∈{1,2,…,8},均有$\frac{{a}_{i+1}}{{a}_{i}}$∈{2,1,-$\frac{1}{2}$},记S=$\frac{{a}_{2}}{{a}_{1}}$+$\frac{{a}_{3}}{{a}_{2}}$+…+$\frac{{a}_{9}}{{a}_{8}}$,则S的最小值为( )
| A. | 5 | B. | 5$\frac{1}{2}$ | C. | 6 | D. | 6$\frac{1}{2}$ |
15.复数$z=\frac{i}{1-i}$在复平面上表示的点在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
5.变量x、y满足条件$\left\{\begin{array}{l}x-y+1≤0\\ y≤1\\ x>-1\end{array}\right.$,则(x-2)2+y2的最小值为( )
| A. | $\frac{{3\sqrt{2}}}{2}$ | B. | $\sqrt{5}$ | C. | 5 | D. | $\frac{9}{2}$ |
12.复数${({\frac{1-i}{{\sqrt{2}}}})^{2015}}$计算的结果是( )
| A. | -1 | B. | -i | C. | $\frac{1+i}{{\sqrt{2}}}$ | D. | $\frac{-1+i}{{\sqrt{2}}}$ |