题目内容
4.已知函数f(x)=log22x-mlog2x+a,g(x)=x2+1.(1)当a=1时,求f(x)在x∈[1,4]上的最小值;
(2)当a>0,m=2时,若对任意的实数t∈[1,4],均存在xi∈[1,8](i=1,2),且x1≠x2,使得$\frac{g({x}_{i}-a)+2a}{{x}_{i}}$=f(t)成立,求实数a的取值范围.
分析 (1)$f(x)=lo{g}_{2}^{2}x-mlo{g}_{2}x+1=(lo{g}_{2}x-\frac{m}{2})^{2}$$+1-\frac{{m}^{2}}{4}$,转化成二次函数问题,利用单调性研究最小值.
(2)令log2t=u(0≤u≤2),则f(t)=u2-2u+a的值域是[a-1,a].由条件列式求解.
解答 解:(1)$f(x)=lo{g}_{2}^{2}x-mlo{g}_{2}x+1=(lo{g}_{2}x-\frac{m}{2})^{2}$$+1-\frac{{m}^{2}}{4}$,其中
0≤log2x≤2. 所以①$\frac{m}{2}≤0$,即m≤0,此时f(x)min=f(1)=1,②当$\frac{m}{2}≥2$,
即m≥4,此时f(x)min=f(4)=5-2m,③0<m<4时,当$lo{g}_{2}x=\frac{m}{2}$时,
$f(x)_{min}=1-\frac{{m}^{2}}{4}$.
所以,f(x)min=$\left\{\begin{array}{l}{1,m≤0}\\{5-2m,m≥4}\\{1-\frac{{m}^{2}}{4},0<m<4}\end{array}\right.$ …(6分)
(2)令log2t=u(0≤u≤2),则f(t)=u2-2u+a的值域是[a-1,a].
∵对任意的实数t∈[1,4],均存在xi∈[1,8](i=1,2),且x1≠x2,使得$\frac{g({x}_{i}-a)+2a}{{x}_{i}}$=f(t)成立,
∴y=$\frac{(x-a)^{2}+1+2a}{x}=x+\frac{(a+1)^{2}}{x}-2a(1≤x≤8)$的值域是[a-1,a].
∴$\left\{\begin{array}{l}{1<a+1<8}\\{a-1>2}\\{a≤{a}^{2}+2}\\{a≤8+\frac{1}{8}(a+1)^{2}-2a}\end{array}\right.$,即$\left\{\begin{array}{l}{0<a<7}\\{a>3}\\{a∈R}\\{a≥11+2\sqrt{14,},a≤11-2\sqrt{14}}\end{array}\right.$,
解得$3<a≤11-2\sqrt{14}$…(14分)
点评 本题主要考查以对数函数为背景的二次函数问题,属于中档题目,高考常考题型.

 名校课堂系列答案
名校课堂系列答案| A. | Φ | B. | [-2,2] | C. | [-1,1] | D. | {-1,1} |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
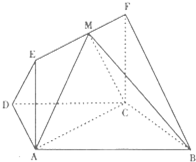 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.