��Ŀ����
16��ijƤЬ���ӽ���1�·ݿ�ʼͶ��������ǰ4���µIJ����ֱ�Ϊ�����ʾ| �·� | 1 | 2 | 3 | 4 |
| ��������˫�� | 1.02 | 1.10 | 1.16 | 1.18 |
���� �ֱ������������ĵ������������������е�δ֪�����������Ƚ����ý��ۣ�
��� 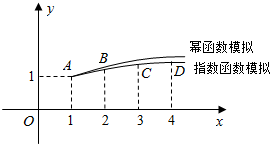 �⣺��y=a$\sqrt{x}$+b������A��D���������֪��
�⣺��y=a$\sqrt{x}$+b������A��D���������֪��
$\left\{\begin{array}{l}{1.02=a+b}\\{1.18=2a+b}\end{array}\right.$����ã�$\left\{\begin{array}{l}{a=0.16}\\{b=0.86}\end{array}\right.$��
��y=0.16$\sqrt{x}$+0.86��
����B��C���������ɵã�yB=$0.16\sqrt{2}+0.86$��1.09��
yC=$0.16\sqrt{3}+0.86$��1.14��
�ֱ���ʵ�����Ϊ0.01��0.02��
��y=abx+c������A��B��C���������֪��
$\left\{\begin{array}{l}{1.02=ab+c}\\{1.10=a{b}^{2}+c}\\{1.16=a{b}^{3}+c}\end{array}\right.$����ã�$\left\{\begin{array}{l}{a=-\frac{32}{75}}\\{b=\frac{3}{4}}\\{c=\frac{67}{50}}\end{array}\right.$��
��y=-$\frac{32}{75}$•$��\frac{3}{4}��^{x}$+$\frac{67}{50}$��
����D�������ɵã�yD=-$\frac{32}{75}$•$��\frac{3}{4}��^{4}$+$\frac{67}{50}$=1.205��
��ʵ�����Ϊ0.025��
�Ƚ�����2��ģ�⺯�������ӣ���Ҫ���ǵ�ʣ��������С����Ҫ����������ʵ�����⣬�������������ƺͿ����ԣ�������Ϊy=0.16$\sqrt{x}$+0.86��ѣ�һ�����ֵ��С�����������½�������ʼ���Ź��˼���������Ч������ߣ�һ��ʱ���ڲ�����������������һ��ʱ�ں��豸�����£���ô������ȻҪ�����ȶ�����Ϊy=0.16$\sqrt{x}$+0.86ǡ�÷�ӳ���������ƣ����ѡ��Ϊy=0.16$\sqrt{x}$+0.86�ȽϽӽ���ʵ�ʣ�
���� ���⿼�麯��ģ�͵�ѡ����Ӧ�ã������������������ע����ⷽ���Ļ��ۣ������е��⣮

 �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д� ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�| A�� | 2 | B�� | 4 | C�� | 8 | D�� | $\frac{17}{2}$ |
| A�� | 0⊆{0} | B�� | 0��{0} | C�� | 0={0} | D�� | 0∉{0} |