题目内容
已知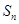 为等差数列
为等差数列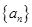 的前
的前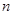 项和,且
项和,且 .
.
(Ⅰ)求数列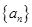 的通项公式;
的通项公式;
(Ⅱ)求数列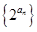 的前
的前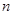 项和公式.
项和公式.
(Ⅰ)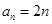 ;(Ⅱ)数列
;(Ⅱ)数列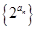 的前
的前 项和
项和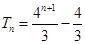 .
.
解析试题分析:(1)求等差数列 的通项公式,一般是将问题中涉及的等式用首项
的通项公式,一般是将问题中涉及的等式用首项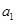 和公差
和公差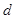 的方程组表示出来并求解,然后利用等差数列的通项公式
的方程组表示出来并求解,然后利用等差数列的通项公式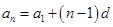 即可求出等差数列
即可求出等差数列 的通项公式;(2)在对数列
的通项公式;(2)在对数列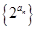 利用公式求前
利用公式求前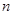 项和时,一般先利用定义法判断它是等差数列还是等比数列,然后再借助相应的公式即可求出数列
项和时,一般先利用定义法判断它是等差数列还是等比数列,然后再借助相应的公式即可求出数列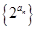 的前
的前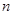 项和.
项和.
试题解析:解(Ⅰ)设等差数列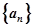 的公差为
的公差为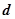 ,
,
因为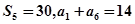
所以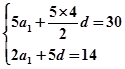
解得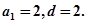
所以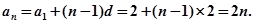 7分
7分
(Ⅱ)由(Ⅰ)可知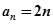 ,令
,令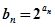
则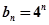 ,
,
又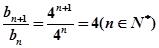
所以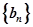 是以4为首项,4为公比的等比数列,
是以4为首项,4为公比的等比数列,
设数列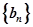 的前
的前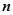 项和为
项和为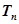
则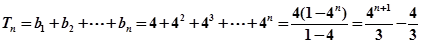
13分
考点:等差数列的通项公式、等比数列的前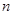 项和
项和

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 ,求数列
,求数列 的前n项和.
的前n项和.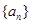 满足
满足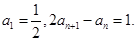
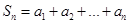
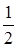 的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n
的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n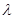 ·bn+1(
·bn+1(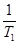 +
+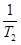 +
+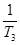 + +
+ +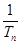 与
与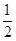 Sn的大小.
Sn的大小. 中,
中, ,
, .
. 满足
满足 ,数列
,数列 项和为
项和为 ,若不等式
,若不等式 对一切
对一切 恒成立,求
恒成立,求 的取值范围.
的取值范围.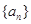 的所有项均为正数,首项
的所有项均为正数,首项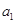 =1,且
=1,且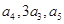 成等差数列.
成等差数列.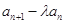 }的前
}的前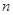 项和为
项和为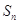 ,若
,若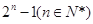 ,求实数
,求实数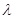 的值.
的值. 中,
中,
 ;
;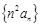 的前
的前 项和
项和 ;
; ,使得
,使得 成立,求实数
成立,求实数 的最小值.
的最小值.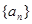 的前n项和
的前n项和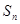 ,且
,且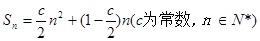 ,且
,且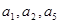 成公比不等于1的等比数列。
成公比不等于1的等比数列。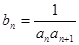 ,求数列{
,求数列{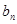 }的前n项和Tn.
}的前n项和Tn. 是等比数列
是等比数列 的前
的前 项和,且
项和,且 ,
, .
. ;
; ,求数列
,求数列 的前
的前 .
.