题目内容
已知数列 中,
中,
(Ⅰ)求数列 的通项
的通项 ;
;
(Ⅱ)求数列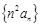 的前
的前 项和
项和 ;
;
(Ⅲ)若存在 ,使得
,使得 成立,求实数
成立,求实数 的最小值.
的最小值.
(Ⅰ)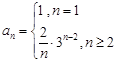 .
.
(Ⅱ) .
.
(Ⅲ)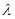 的最小值是
的最小值是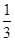 .
.
解析试题分析:(Ⅰ)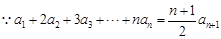 ,
, ①
①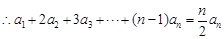 ,
,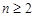 ②
②
①-②: ,
,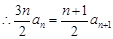 , 2分
, 2分
即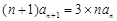 (
(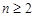 ),又
),又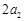 =2,
=2,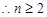 时,数列
时,数列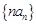 是以2为首项,3为公比的等比数列.
是以2为首项,3为公比的等比数列.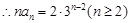 ,故
,故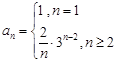 4分
4分
(Ⅱ)由(Ⅰ)可知当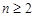 时,
时,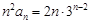 ,
,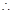 当
当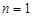 时,
时,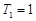 ;
;
当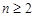 时,
时,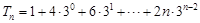 ,①
,①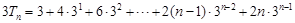 ,②
,②
①-②得,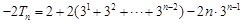
=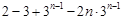
=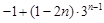
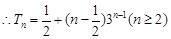 ,又
,又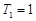 也满足
也满足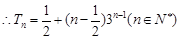 9分
9分
(Ⅲ)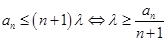 ,由(Ⅰ)可知:
,由(Ⅰ)可知:
当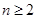 时,
时,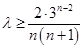 ,令
,令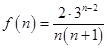 ,
,
则 ,
,
又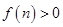 ,∴
,∴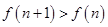
∴当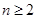 时,
时,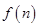 单增,∴
单增,∴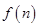 的最小值是
的最小值是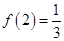
而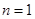 时,
时,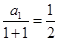 ,综上所述,
,综上所述,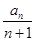 的最小值是
的最小值是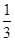
∴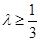 ,即
,即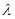 的最小值是
的最小值是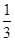 13分
13分
考点:等差数列、等比数列的通项公式及其求和公式,“错位相减法”,不等式恒成立问题。
点评:难题,为确定等差数列、等比数列的通项公式,往往通过建立相关元素的方程组,而达到目的。数列的求和问题,往往涉及“公式法”“分组求和法”“裂项相消法”“错位相减法”等。涉及不等式恒成立问题,通过放缩、求和等,得到最值。

练习册系列答案
相关题目
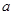 为实数,数列
为实数,数列 满足
满足 ,当
,当 时,
时, ,
,  ;(5分)
;(5分) ,使
,使 ;(5分)
;(5分) ,当
,当 时,求证:
时,求证: (6分)
(6分)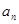 }的前
}的前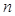 项和为
项和为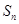 ,已知对任意的
,已知对任意的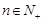 ,点
,点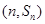 ,均在函数
,均在函数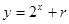 的图像上.
的图像上. 的值;
的值; 求数列
求数列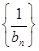 的前
的前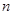 项和
项和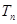 .
.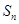 为等差数列
为等差数列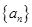 的前
的前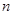 项和,且
项和,且 .
.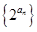 的前
的前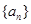 为等比数列, 其前
为等比数列, 其前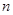 项和为
项和为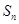 , 已知
, 已知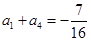 , 且对于任意的
, 且对于任意的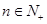 有
有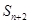 ,
, 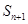 成等差;求数列
成等差;求数列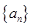 中,
中,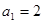 ,
,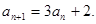
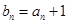 ,求证:数列
,求证:数列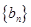 为等比数列;
为等比数列;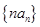 的前
的前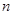 项和
项和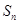
 中,
中, ,公差
,公差 为整数,若
为整数,若 ,
, .
. 。
。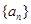 中,
中,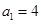 ,
, 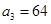 .
.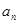 ;
; 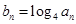 ,求数列
,求数列 的前n项和
的前n项和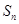 ;
;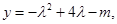 对于(2)中的
对于(2)中的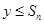 对一切正整数n及任意实数
对一切正整数n及任意实数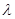 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. 对任意
对任意 ,满足
,满足 (
( 为常数),称数列
为常数),称数列 项和
项和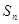 满足
满足 ,求
,求 ,数列
,数列 的前
的前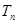 , 求证:
, 求证: .
.