题目内容
6.已知集合A={-2≤x≤3},B={x|m+1≤x≤2m-1}.(1)若B⊆A,求m的取值集合;
(2)若A⊆B,求m的取值集合;
(3)是否存在实数m,使得A=B?若存在,求出m的值;若不存在,请说明理由.
分析 理清集合A、B的关系,得到关于m的不等式,解得即可求实数m的取值范围.
解答 解:(1)集合A={-2≤x≤3},B={x|m+1≤x≤2m-1},且B⊆A
①B=∅时,m+1>2m-1,故m<2;
②B≠∅时,m≥2,且$\left\{\begin{array}{l}{m+1≥-2}\\{2m-1≤3}\end{array}\right.$,∴m=2;
故m≤2;
(2)集合A={-2≤x≤3},B={x|m+1≤x≤2m-1},且A⊆B,
∴$\left\{\begin{array}{l}{m+1≤-2}\\{2m-1≥3}\\{m+1≤2m-1}\end{array}\right.$,
解得m∈∅;
(3)若A=B,则m+1=-2且2m-1=3,解得m∈∅.
点评 本题主要考查集合的相等等基本运算,属于基础题.要正确判断两个集合间相等的关系,必须对集合的相关概念有深刻的理解,善于抓住代表元素,认清集合的特征.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
17.若圆M在x轴与y轴上截得的弦长总相等,则圆心M的轨迹方程是( )
| A. | x-y=0 | B. | x+y=0 | C. | x2+y2=0 | D. | x2-y2=0 |
14.下列等式中,一定正确的是( )
| A. | a${\;}^{\frac{m}{n}}$=($\root{n}{a}$)m | B. | -a${\;}^{\frac{m}{n}}$=$\root{n}{(-a)^{n}}$ | C. | a${\;}^{-\frac{m}{n}}$=$\root{m}{{a}^{n}}$ | D. | a${\;}^{-\frac{m}{n}}$=$\root{n}{{a}^{-m}}$ |
7.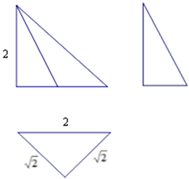 一个几何体的三视图如图.该几何体的各个顶点都在球O的球面上,球O的体积为( )
一个几何体的三视图如图.该几何体的各个顶点都在球O的球面上,球O的体积为( )
 一个几何体的三视图如图.该几何体的各个顶点都在球O的球面上,球O的体积为( )
一个几何体的三视图如图.该几何体的各个顶点都在球O的球面上,球O的体积为( )| A. | $\frac{\sqrt{2}}{3}$π | B. | $\frac{4\sqrt{2}}{3}$π | C. | $\frac{8\sqrt{2}}{3}$π | D. | $\frac{10\sqrt{2}}{3}$π |