题目内容
【题目】已知集合A＝{x|1＜x＜6}，B＝{x|2＜x＜10}，C＝{x|5﹣a＜x＜a}．
（1）求A∪B，（RA）∩B；
（2）若CB，求实数a的取值范围．
【答案】（1）A∪B＝{x|1＜x＜10},（RA）∩B＝{x|6≤x＜10} ；（2）
.
【解析】
（1）进行并集、交集和补集的运算即可；
（2）根据CB，可讨论C是否为空集：C＝时，5﹣a≥a；C≠时，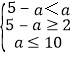
，这样即可得出实数a的取值范围．
（1）∵A＝{x|1＜x＜6}，B＝{x|2＜x＜10}，
A∪B＝{x|1＜x＜10}，RA＝{x|x≤1，或x≥6}；
∴（RA）∩B＝{x|6≤x＜10}；
（2）∵CB；
①C＝时，5﹣a≥a；
∴
；
②C≠时，则；
解得
；
综上得，a≤3；
∴a的取值范围是（﹣∞，3]．
练习册系列答案
相关题目
【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费
（单位：千元）对年销售量
（单位：
）和年利润
（单位：千元）的影响，对近13年的宣传费
和年销售量
数据作了初步处理，得到散点图及一些统计量的值．
由散点图知，按
建立关于的回归方程是合理的．令
，则
，经计算得如下数据：
|
|
|
|
|
|
10.15 | 109.94 | 0.16 | -2.10 | 0.21 | 21.22 |
最小二乘法求线性回归方程系数公式
（Ⅰ）根据以上信息，建立关于
的回归方程；
（Ⅱ）已知这种产品的年利润与
的关系为
．根据（1）的结果，求当年宣传费
时，年利润的预报值是多少？