题目内容

1．“a=1”是“直线x-ay-2=0与直线2ax-（a-3）y+1=0垂直”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不不必要条件

分析 根据直线垂直的条件，结合充分条件和必要条件的定义进行判断即可．

解答 解：∵“直线x-ay-2=0与直线2ax-（a-3）y+1=0垂直”的充要条件是“2a+a（a-3）=0也就是a=0或a=1”，
所以“a=1”是“直线x-ay-2=0与直线2ax-（a-3）y+1=0垂直”的充分不必要条件．
故选：A．

点评 本题主要考查充分条件和必要条件的应用，利用直线垂直的条件是解决本题的关键．

练习册系列答案
相关题目
11．已知函数f（x）的导数f′（x）=a[x2+（1-a）x-a]（a≠0），若函数f（x）在x=a处取到极大值，则实数a的取值范围是（-1，0）．
12．等比数列{an}（an＞0，n∈N*）中，公比q∈（0，1），a1a5+2a3a5+a2a8=25，且2是a3与a5的等比中项．
（1）求数列{an}的通项公式；
（2）设bn=log2an，数列{bn}的前n项和为Sn，当n≥2时，比较Sn与bn的大小．
9．已知f（x）=3sinx-πx，对任意的x∈（0，$\frac{π}{2}$），给出以下四个结论：
①f′（x）＞0；
②f′（x）＜0；
③f（x）＞0；
④f（x）＜0．
其中正确的是（　　）
A．①③B．①④C．②③D．②④
16．已知函数f（x）=2sin（x-π）cos（π-x），则f（x）的最小正周期为π，在区间[-$\frac{π}{6}，\frac{π}{2}$]的最小值是-$\frac{\sqrt{3}}{2}$．
6．已知a、b、c分别为△ABC三个内角A，B，C的对边，若A=$\frac{π}{3}$，则a（cosC+$\sqrt{3}$sinC）=（　　）
A．a+bB．b+cC．a+cD．a+b+c
13．执行如图所示的程序框图，则输出结果S=（　　）
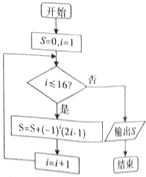
A．14B．16C．19D．21
10．定义[x]表示不超过x的最大整数（x∈R），如：[-1，3]=-2，[0，8]=0；定义{x}=x-[x]．
（1）{$\frac{999}{1000}$}+{$\frac{99{9}^{2}}{1000}$}+{$\frac{99{9}^{3}}{1000}$}+{$\frac{99{9}^{4}}{1000}$}=2；
（2）当n为奇数时，
{$\frac{999}{1000}$}+{$\frac{99{9}^{2}}{1000}$}+{$\frac{99{9}^{3}}{1000}$}+…+{$\frac{99{9}^{n}}{1000}$}=$\frac{n-1}{2}+\frac{999}{1000}$．
11．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线平行于直线l：y=2x+10，双曲线的一个焦点在直线l上，则双曲线的方程为（　　）
A．$\frac{{3{x^2}}}{25}-\frac{{3{y^2}}}{100}=1$B．$\frac{{3{x^2}}}{100}-\frac{{3{y^2}}}{25}=1$
C．$\frac{x^2}{20}-\frac{y^2}{5}=1$D．$\frac{x^2}{5}-\frac{y^2}{20}=1$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网