题目内容
【题目】如图,三棱柱ABC﹣A1B1C1中,侧棱与底面垂直,AB=AC=1,AA1=2,且P,Q,M分别是BB1 , CC1 , B1C1的中点,AB⊥AQ. 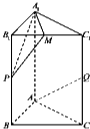
(1)求证:AB⊥AC;
(2)求证:AQ∥平面A1PM;
(3)求AQ与平面BCC1B1所成角的大小.
【答案】
(1)证明:∵A1A⊥面ABC,而AB面ABC,∴AB⊥A1A,
又∵AB⊥AQ,
∴AB⊥面ACC1A1,
又∵AC面ACC1A1,
∴AB⊥AC
(2)证明:取BC的中点G,连接AG、QG、BC1,
∵P、M分别是BB1、B1C1的中点,
∴MP∥BC1,
同理:QG∥BC1,
∴QG∥MP,
又∵M为B1C1的中点,G为BC中点,
∴A1M∥AG,
又∵QG∥MP,
∴面APQ∥面A1PM,
∴AQ∥平面A1PM
(3)解:取BC的中点G,连接AG、DG,
∵AB=AC=1,
∴AG⊥BC,
又∵AG⊥BB1,
∴AG⊥面BCC1B1,
故∠AQG为直线AQ与平面BCC1B1所成角,
在△ABC中,∠ABC=90°,AB=AC=1,则BC= ![]() 且AG=
且AG= ![]() ,
,
在Rt△AQG中,AG= ![]() ,GQ=
,GQ= ![]() =
= ![]() ,
,
则tan∠AQG= ![]() =
= ![]() ,
,
则∠AQG=30°.
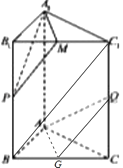
【解析】(1)由于三棱柱中侧棱与底面垂直,分析可得AB⊥A1A,又由题干条件AB⊥AQ,由线面垂直的判定定理即可得证明;(2)取BC的中点G,连接AG、QG、BC1 , 由中位线的性质可得可得MP∥BC1与QG∥BC1 , 进而可得QG∥MP,分析可得A1M∥AG,由面面平行的判定方法可得面APQ∥面A1PM,进而结合面面平行的性质可得证明;(3)取BC的中点G,连接AG、DG,分析易得AG⊥面BCC1B1 , 进而由线面角的定义可得∠AQG为直线AQ与平面BCC1B1所成角;在△ABC中分析可得BC= ![]() AG=
AG= ![]() ,进而在Rt△AQG中,计算可得AG=
,进而在Rt△AQG中,计算可得AG= ![]() ,GQ=
,GQ= ![]() =
= ![]() ,由正切的定义可得tan∠AQG=
,由正切的定义可得tan∠AQG= ![]() =
= ![]() ,计算即可得答案.
,计算即可得答案.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则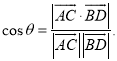 .
.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案