题目内容
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗,2020年春节前夕,A市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
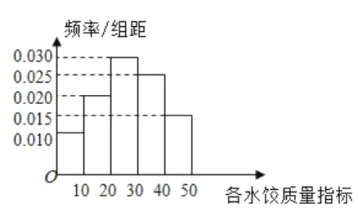
(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在
落在![]() 内的概率;
内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于![]() 内的包数为
内的包数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.
【答案】(1)26.5;(2)①0.1359;②分布列详见解析,数学期望为2.
【解析】
(1)根据频率分布直方图分别计算各组的频率,再计算平均值即可;
(2)①直接由正态分布的性质及题目所给可得;
②根据题意得![]() ,根据二项分布的性质即可求得
,根据二项分布的性质即可求得![]() 的分布列、期望值.
的分布列、期望值.
(1)根据频率分布直方图可得各组的频率为:
![]() 的频率为:
的频率为:![]() ;
;
![]() 的频率为:
的频率为:![]() ;
;
![]() 的频率为:
的频率为:![]() ;
;
![]() 的频率为:
的频率为:![]() ;
;
![]() 的频率为:
的频率为:![]() ,
,
所以所抽取的100包速冻水饺该项质量指标值的样本平均数![]() 为
为
![]() .
.
(2)①∵![]() 服从正态分布
服从正态分布![]() ,且
,且![]() ,
,![]()
![]()
![]()
![]()
∴![]() 落在
落在![]() 内的概率是0.1359.
内的概率是0.1359.
②根据题意得每包速冻水饺的质量指标值位于![]() 内的概率为
内的概率为![]() ,
,
所以![]() ,
,
![]() 的可能取值分别为:0,1,2,3,4,
的可能取值分别为:0,1,2,3,4,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
∴![]() .
.

练习册系列答案
相关题目

