题目内容
P点在椭圆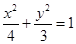 上运动,Q,R分别在两圆
上运动,Q,R分别在两圆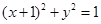 和
和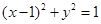 上运动,则|PQ|+|PR|的最大值为 .
上运动,则|PQ|+|PR|的最大值为 .
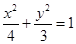 上运动,Q,R分别在两圆
上运动,Q,R分别在两圆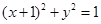 和
和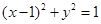 上运动,则|PQ|+|PR|的最大值为 .
上运动,则|PQ|+|PR|的最大值为 .
解:∵椭圆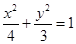 中,c2=4-3=1,
中,c2=4-3=1,
∴椭圆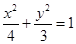 两焦点F1(-1,0),F2(1,0)恰为两圆(
两焦点F1(-1,0),F2(1,0)恰为两圆(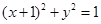 和(
和(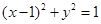 的圆心,e=
的圆心,e=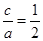 ,准线x=
,准线x=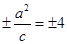
过P点作x轴平行线,分别交两准线于A,B两点,
连接PF1,PF2,并延长,分别交两圆于Q‘,R’,
则|PQ|+|PR|≤|PQ‘|+|PR’|
=|PF1|+1+|PF2|+1
=e|PA|+e|PB|+2
=e|AB|+2
= 1 2 ×8+2
1 2 ×8+2
=6.
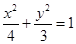 中,c2=4-3=1,
中,c2=4-3=1,∴椭圆
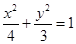 两焦点F1(-1,0),F2(1,0)恰为两圆(
两焦点F1(-1,0),F2(1,0)恰为两圆(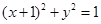 和(
和(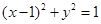 的圆心,e=
的圆心,e=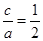 ,准线x=
,准线x=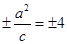
过P点作x轴平行线,分别交两准线于A,B两点,
连接PF1,PF2,并延长,分别交两圆于Q‘,R’,
则|PQ|+|PR|≤|PQ‘|+|PR’|
=|PF1|+1+|PF2|+1
=e|PA|+e|PB|+2
=e|AB|+2
=
 1 2 ×8+2
1 2 ×8+2=6.

练习册系列答案
相关题目
 的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足
的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足 点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
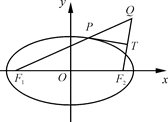
 为点P的横坐标,证明
为点P的横坐标,证明 ;
; 的面积S=
的面积S= 若存在,求∠F1MF2的正切值;若不存在,请说明理由.
若存在,求∠F1MF2的正切值;若不存在,请说明理由. 方程为:
方程为: .
. 过点
过点 ,且与圆
,且与圆 、
、 两点,若
两点,若 ,求直线
,求直线 作平行于
作平行于 轴的直线
轴的直线 ,设
,设 轴的交点为
轴的交点为 ,若向量
,若向量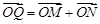 ,求动点
,求动点 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线. 的离心率
的离心率 ,过
,过 、
、 两点的直线到原点的距离是
两点的直线到原点的距离是 .
. 交椭圆于不同的两点
交椭圆于不同的两点 、
、 ,且
,且 为圆心的圆上,求
为圆心的圆上,求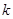 的值.
的值. 的离心率为
的离心率为 ,过右焦点F且斜率为
,过右焦点F且斜率为 的直线与
的直线与 相交于A、B两点,若
相交于A、B两点,若 ,则
,则 =
= C、
C、 D、2
D、2 上的动点,F1,F2分别为其左、右焦点,O是坐标原点,则
上的动点,F1,F2分别为其左、右焦点,O是坐标原点,则 的取值范围是 .
的取值范围是 .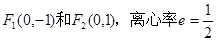
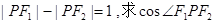 的值
的值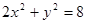 的长轴长是( )
的长轴长是( )


 的准线与
的准线与 轴交于
轴交于 ,焦点为
,焦点为 ,以
,以 的椭圆的两条准线之间的距离为 ( )
的椭圆的两条准线之间的距离为 ( )