题目内容
已知椭圆 的离心率为
的离心率为 ,过右焦点F且斜率为
,过右焦点F且斜率为 的直线与
的直线与 相交于A、B两点,若
相交于A、B两点,若 ,则
,则 =
=
A、1 B、 C、
C、 D、2
D、2
 的离心率为
的离心率为 ,过右焦点F且斜率为
,过右焦点F且斜率为 的直线与
的直线与 相交于A、B两点,若
相交于A、B两点,若 ,则
,则 =
=A、1 B、
 C、
C、 D、2
D、2B
解:A(x1,y1),B(x2,y2),
∵ AF ="3" FB ,∴y1=-3y2,
∵e= ,设a=2t,c=
,设a=2t,c=  t,b=t,
t,b=t,
∴x2+4y2-4t2=0,直线AB方程为x="sy+" t.代入消去x,
t.代入消去x,
∴(s2+4)y2+2 sty-t2=0,
sty-t2=0,
∴y1+y2=-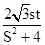 ,y1y2=-
,y1y2=- ,-2y2=-
,-2y2=-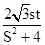 ,-3y 22 =-
,-3y 22 =- ,
,
解得s2= ,k=
,k=  故选B
故选B
∵ AF ="3" FB ,∴y1=-3y2,
∵e=
 ,设a=2t,c=
,设a=2t,c=  t,b=t,
t,b=t,∴x2+4y2-4t2=0,直线AB方程为x="sy+"
 t.代入消去x,
t.代入消去x,∴(s2+4)y2+2
 sty-t2=0,
sty-t2=0,∴y1+y2=-
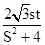 ,y1y2=-
,y1y2=- ,-2y2=-
,-2y2=-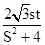 ,-3y 22 =-
,-3y 22 =- ,
,解得s2=
 ,k=
,k=  故选B
故选B
练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 :
: 的离心率为
的离心率为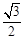 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切. ,
, 、
、 是椭圆
是椭圆 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆 ,求直线
,求直线 与
与 的两个焦点F1、F2,点P在椭圆C上,且P F1⊥F1F2,| P F1|=
的两个焦点F1、F2,点P在椭圆C上,且P F1⊥F1F2,| P F1|= ,| P F2|=
,| P F2|=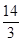 。
。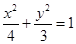 上运动,Q,R分别在两圆
上运动,Q,R分别在两圆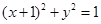 和
和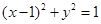 上运动,则|PQ|+|PR|的最大值为 .
上运动,则|PQ|+|PR|的最大值为 . 个单位距离,城际快速通道所在的曲线为E,使快速通道E上的点到两区的距离之和为4个单位距离.
个单位距离,城际快速通道所在的曲线为E,使快速通道E上的点到两区的距离之和为4个单位距离.
 的笔直公路l与曲线E交于P,Q两点,同时在曲线E上建一个加油站M(横坐标为负值)满足
的笔直公路l与曲线E交于P,Q两点,同时在曲线E上建一个加油站M(横坐标为负值)满足 ,求
,求 面积的最大值.
面积的最大值. 
 的右焦点为F,过F且斜率为
的右焦点为F,过F且斜率为 的直线交C于A、B两点,若
的直线交C于A、B两点,若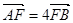 ,则C的离心率为
,则C的离心率为  的一个焦点为F(2,0),离心率
的一个焦点为F(2,0),离心率 .
. 与椭圆交于不同的A,B两点,与y轴交于E点,且
与椭圆交于不同的A,B两点,与y轴交于E点,且 ,求实数m的值.
,求实数m的值.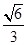 的椭圆
的椭圆
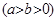 经过点
经过点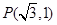 .
.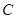 的方程;
的方程; 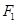 且不与
且不与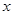 轴垂直的直线
轴垂直的直线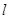 交椭圆
交椭圆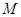 、
、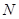 两点,若
两点,若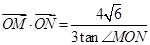 (
(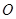 为坐标原点),求直线
为坐标原点),求直线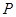 是椭圆
是椭圆 上一点,
上一点, 和
和 是椭圆的两个焦点,则
是椭圆的两个焦点,则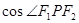 的最小值是( )
的最小值是( )


