题目内容
已知椭圆的焦点是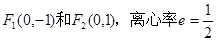
(1)求此椭圆的标准方程
(2)设点P在此椭圆上,且有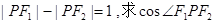 的值
的值
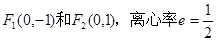
(1)求此椭圆的标准方程
(2)设点P在此椭圆上,且有
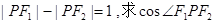 的值
的值(1)
(2)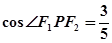

(2)
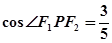
(1) 由焦点坐标可得c值,根据离心率可求a,再利用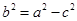 求出b2的值,椭圆方程得解.
求出b2的值,椭圆方程得解.
(2)根据椭圆的定义得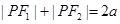 ,
,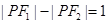 ,可解出
,可解出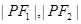 ,
,
又知道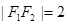 ,利用余弦定理可求
,利用余弦定理可求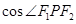 .
.
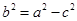 求出b2的值,椭圆方程得解.
求出b2的值,椭圆方程得解.(2)根据椭圆的定义得
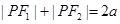 ,
,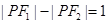 ,可解出
,可解出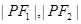 ,
,又知道
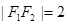 ,利用余弦定理可求
,利用余弦定理可求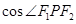 .
.
练习册系列答案
相关题目
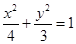 上运动,Q,R分别在两圆
上运动,Q,R分别在两圆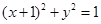 和
和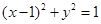 上运动,则|PQ|+|PR|的最大值为 .
上运动,则|PQ|+|PR|的最大值为 .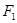 、
、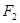 是椭圆
是椭圆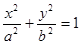 的两个焦点,O为坐标原点,点
的两个焦点,O为坐标原点,点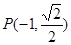 在椭圆上,线段
在椭圆上,线段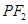 与
与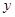 轴的交点
轴的交点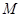 满足
满足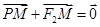 ;⊙O是以F1F2为直径的圆,一直线l:
;⊙O是以F1F2为直径的圆,一直线l: 与⊙O相切,并与椭圆交于不同的两点A、B.
与⊙O相切,并与椭圆交于不同的两点A、B.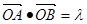 且满足
且满足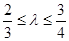 时,求△AOB面积S的取值范围.
时,求△AOB面积S的取值范围.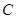 以
以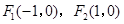 为焦点,且离心率
为焦点,且离心率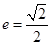 .
. 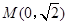 点斜率为
点斜率为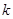 的直线
的直线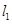 与椭圆
与椭圆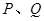 ,求
,求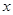 轴正半轴、
轴正半轴、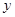 轴正半轴的交点分别为
轴正半轴的交点分别为 ,是否存在直线
,是否存在直线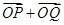 与
与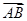 垂直?如果存在,写出
垂直?如果存在,写出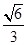 的椭圆
的椭圆
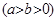 经过点
经过点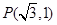 .
.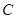 的方程;
的方程; 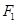 且不与
且不与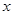 轴垂直的直线
轴垂直的直线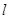 交椭圆
交椭圆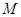 、
、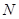 两点,若
两点,若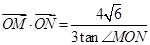 (
(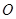 为坐标原点),求直线
为坐标原点),求直线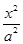 +
+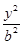 =1(a>b>c>0,a2=b2+c2)的左右焦点分别为F1,F2,若以F2为圆心,b―c为半径作圆F2,过椭圆上一点P作此圆的切线,切点为T,且|PT|的最小值为
=1(a>b>c>0,a2=b2+c2)的左右焦点分别为F1,F2,若以F2为圆心,b―c为半径作圆F2,过椭圆上一点P作此圆的切线,切点为T,且|PT|的最小值为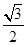 (a―c),则椭圆的离心率e的取值范围是 .
(a―c),则椭圆的离心率e的取值范围是 .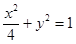 的左焦点为
的左焦点为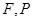 为椭圆上一点,其横坐标为
为椭圆上一点,其横坐标为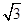 ,则
,则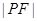 =( )
=( ) 



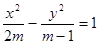 表示焦点在y轴上的椭圆;命题q:双曲线
表示焦点在y轴上的椭圆;命题q:双曲线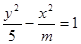 的离心率
的离心率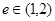 ,若p、q有且只有一个为真,求m的取值范围。
,若p、q有且只有一个为真,求m的取值范围。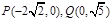 的椭圆标准方程( ).
的椭圆标准方程( ).


