题目内容
已知椭圆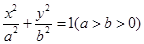 的右准线
的右准线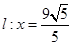 ,离心率
,离心率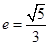 ,
,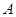 ,
,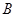 是椭圆上的两动点,动点
是椭圆上的两动点,动点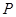 满足
满足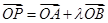 ,(其中
,(其中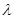 为常数).
为常数).
(1)求椭圆标准方程;
(2)当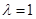 且直线
且直线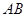 与
与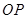 斜率均存在时,求
斜率均存在时,求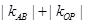 的最小值;
的最小值;
(3)若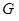 是线段
是线段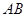 的中点,且
的中点,且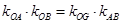 ,问是否存在常数
,问是否存在常数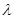 和平面内两定点
和平面内两定点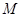 ,
,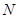 ,使得动点
,使得动点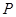 满足
满足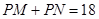 ,若存在,求出
,若存在,求出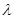 的值和定点
的值和定点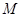 ,
,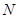 ;若不存在,请说明理由.
;若不存在,请说明理由.
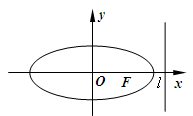
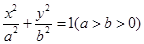 的右准线
的右准线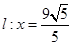 ,离心率
,离心率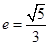 ,
,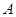 ,
,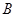 是椭圆上的两动点,动点
是椭圆上的两动点,动点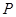 满足
满足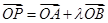 ,(其中
,(其中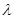 为常数).
为常数).(1)求椭圆标准方程;
(2)当
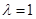 且直线
且直线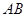 与
与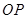 斜率均存在时,求
斜率均存在时,求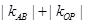 的最小值;
的最小值;(3)若
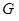 是线段
是线段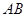 的中点,且
的中点,且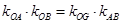 ,问是否存在常数
,问是否存在常数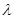 和平面内两定点
和平面内两定点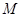 ,
,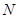 ,使得动点
,使得动点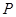 满足
满足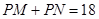 ,若存在,求出
,若存在,求出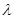 的值和定点
的值和定点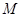 ,
,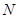 ;若不存在,请说明理由.
;若不存在,请说明理由.
(1)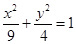 ;(2)
;(2)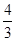 ;(3)
;(3)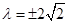 ,
,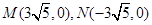
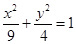 ;(2)
;(2)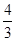 ;(3)
;(3)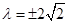 ,
,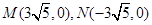
试题分析:(1)根据题意由已知可得:
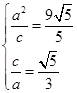 ,进而求出基本量,得到椭圆方程;
,进而求出基本量,得到椭圆方程; 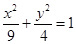 ;(2)由题中
;(2)由题中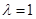 ,可得
,可得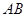 中点与原点的斜率即为
中点与原点的斜率即为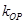 ,即可化简得:
,即可化简得: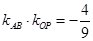 ,结合基本不等式求最值,即由
,结合基本不等式求最值,即由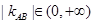 得
得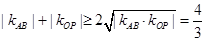 ;(3)由(2)中已求出
;(3)由(2)中已求出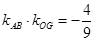 ,即
,即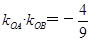 ,可化简得:
,可化简得: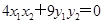 ,再结合条件
,再结合条件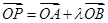 ,代入化简可得:
,代入化简可得: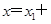
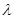
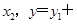
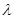
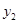 ,最后由点在椭圆上可得:
,最后由点在椭圆上可得: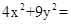
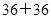
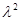
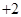
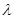
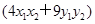 ,即
,即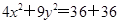
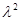 ,化简即P点是椭圆
,化简即P点是椭圆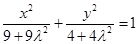 上的点,利用椭圆知识求出左、右焦点为
上的点,利用椭圆知识求出左、右焦点为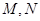 .
.(I)由题设可知:
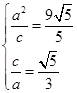 ∴
∴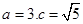 .又
.又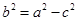 ,∴
,∴ .
.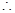 椭圆标准方程为
椭圆标准方程为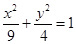 . 5分
. 5分(2)设
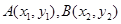 则由
则由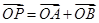 得
得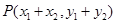 .
.∴
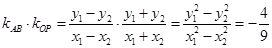 .
. 由
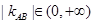 得
得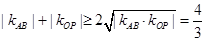 当且仅当
当且仅当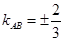 时取等号 10分
时取等号 10分(3)
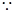
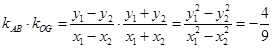 .
.∴
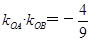 .∴
.∴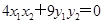 . 11分
. 11分设
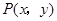 ,则由
,则由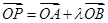 得
得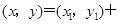
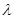
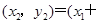
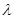
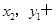
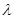
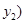 ,
,即
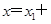
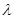
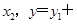
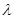 y2. 因为点A、B在椭圆
y2. 因为点A、B在椭圆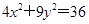 上,
上,所以
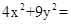
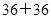
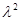
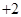
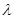
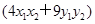 .
.所以
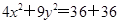
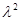 . 即
. 即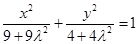 ,所以P点是椭圆
,所以P点是椭圆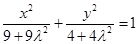 上的点,
上的点,设该椭圆的左、右焦点为
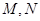 ,,则由椭圆的定义
,,则由椭圆的定义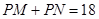 得18
得18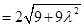 ,
,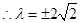 ,
,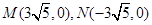 16分
16分
练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
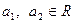 ,
,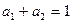 ,求证:
,求证: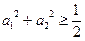 ;
;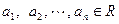 ,
,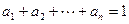 ,求证:
,求证: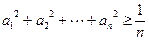 .
.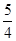 ,则函数y=4x-2+
,则函数y=4x-2+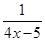 的最大值是 .
的最大值是 .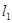 :y=-1,过定点F与直线
:y=-1,过定点F与直线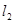 交动点C的轨迹于两点P、Q,交直线
交动点C的轨迹于两点P、Q,交直线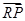 ·
·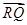 的最小值;
的最小值;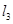 交动点C的轨迹于两点R、T,问四边形PRQT的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
交动点C的轨迹于两点R、T,问四边形PRQT的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.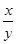 +y)(
+y)(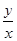 +x)的最小值为________.
+x)的最小值为________.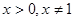 时,
时,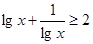
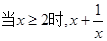 的最小值为
的最小值为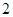
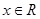 时,
时,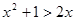
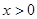 时,
时,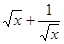 的最小值为
的最小值为 ,且
,且 ,
, ,则
,则 的值是 .
的值是 .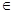 R,2a2-b2=1,则|2a-b|的最小值为 .
R,2a2-b2=1,则|2a-b|的最小值为 .