题目内容
证明以下不等式:
(1)已知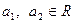 ,
,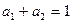 ,求证:
,求证: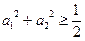 ;
;
(2)若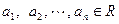 ,
,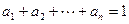 ,求证:
,求证: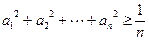 .
.
(1)已知
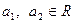 ,
,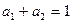 ,求证:
,求证: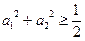 ;
;(2)若
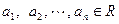 ,
,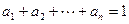 ,求证:
,求证: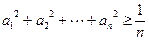 .
.见解析
(1)构造函数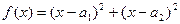
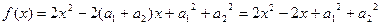
因为对一切xÎR,恒有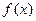 ≥0,所以
≥0,所以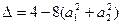 ≤0,
≤0,
从而得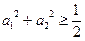
(另解:利用重要不等式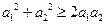 )
)
(2)构造函数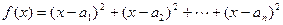
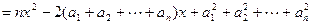
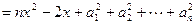
因为对一切xÎR,都有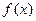 ≥0,所以△=
≥0,所以△=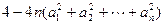 ≤0,
≤0,
从而证得: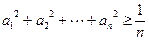 .
.
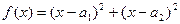
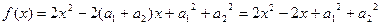
因为对一切xÎR,恒有
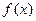 ≥0,所以
≥0,所以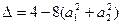 ≤0,
≤0,从而得
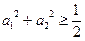
(另解:利用重要不等式
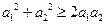 )
)(2)构造函数
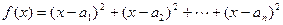
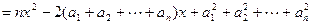
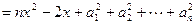
因为对一切xÎR,都有
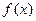 ≥0,所以△=
≥0,所以△=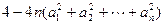 ≤0,
≤0,从而证得:
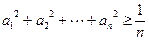 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 +
+ ≥2
≥2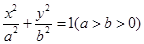 的右准线
的右准线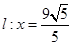 ,离心率
,离心率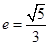 ,
,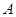 ,
,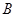 是椭圆上的两动点,动点
是椭圆上的两动点,动点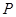 满足
满足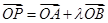 ,(其中
,(其中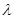 为常数).
为常数).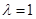 且直线
且直线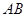 与
与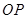 斜率均存在时,求
斜率均存在时,求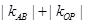 的最小值;
的最小值;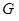 是线段
是线段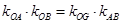 ,问是否存在常数
,问是否存在常数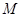 ,
,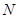 ,使得动点
,使得动点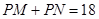 ,若存在,求出
,若存在,求出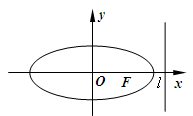
 +
+ 的最小值是________.
的最小值是________.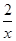 +
+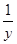 =1,并且2x+y>m恒成立,则实数m的取值范围是 .
=1,并且2x+y>m恒成立,则实数m的取值范围是 .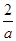 +
+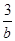 的最小值为________.
的最小值为________.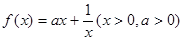 在
在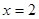 时取得最小值,则
时取得最小值,则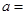 ____________.
____________.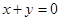 ,则
,则 的最小值是( )
的最小值是( )