Question

【题目】已知函数f（x）＝x2﹣2acoskπlnx（k∈N*，a∈R且a＞0）．

（1）讨论函数f（x）的单调性；

（2）若k＝2018，关于x的方程f（x）＝2ax有唯一解，求a的值；

（3）当k＝2019时，证明：对一切x∈（0，+∞），都有成立．

Answer 1

【答案】（1）见解析；（2）a；（3）证明见解析.

【解析】

（1）求导求出，对分类讨论，求出的解，即可求出结论；

（2）问题转化为只有一个零点，求出函数的极值，根据图像可得极值点即为零点，建立方程关系，即可求出；

（3）根据已知即证xlnx，x＞0恒成立，先考虑证明不等式成立的充分条件，即证明，若不成立，则构造函数，证明，即可证明结论.

（1）由已知得x＞0且f′（x）＝2xcoskπ＝2x﹣．

当k是奇数时，f′（x）＞0，则f（x）在（0，+∞）上是增函数；

当k是偶数时，则f′（x）＝2x．

所以当x∈（0，）时，f′（x）＜0，

当x∈（，+∞）时，f′（x）＞0．

故当k是偶数时，f （x）在（0，）上是减函数，

在（，+∞）上是增函数．

（2）若k＝2018，则f（x）＝x2﹣2alnx．

记g（x）＝f（x）﹣2ax＝x2﹣2alnx﹣2ax，

∴g′（x）（x2﹣ax﹣a），

若方程f（x）＝2ax有唯一解，即g（x）＝0有唯一解；

令g′（x）＝0，得x2﹣ax﹣a＝0．

因为a＞0，x＞0，所以x10（舍去），x2．

当x∈（0，x2）时，g′（x）＜0，g（x）在（0，x2）是单调递减函数；

当x∈（x2，+∞）时，g′（x）＞0，g（x）在（x2，+∞）上是单调递增函数．

当x＝x2时，g′（x2）＝0，g（x）min＝g（x2）．

因为g（x）＝0有唯一解，所以g（x2）＝0．

则 ，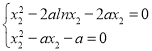

两式相减得2alnx2+ax2﹣a＝0，

又∵a＞0，∴2lnx2+x2﹣1＝0（*）；

设函数h（x）＝2lnx+x﹣1，

因为在x＞0时，h （x）是增函数，所以h （x）＝0至多有一解．

因为h（1）＝0，所以方程（*）的解为x 2＝1，从而解得a．

（3）证明：当k＝2019时，问题等价于证明xlnx，x＞0，

由导数可求φ（x）＝xlnx（x∈（0，+∞））的最小值是，

当且仅当x时取到，

设m（x），则m′（x），

当0＜x＜1时，m′（x）＞0，函数m（x）单调递增，

当x＞1时，m′（x）＜0，函数m（x）单调递减，

∴m（x）max＝m（1）

从而对一切x∈（0，+∞），都有xlnx，成立．故命题成立．