题目内容
【题目】在长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为2的正方形,E是AB的中点,F是BC的中点
(1)求证:EF∥平面A1DC1;
(2)若长方体ABCD﹣A1B1C1D1中,夹在平面A1DC1与平面B1EF之间的几何体的体积为![]() ,求点D到平面B1EF的距离.
,求点D到平面B1EF的距离.

【答案】(1)证明见详解;(2)2![]() .
.
【解析】
(1)因为![]() //
//![]() ,由线线平行,即可推证线面平行;
,由线线平行,即可推证线面平行;
(2)先根据几何体的体积求解出长方体的高,再用等体积法求得点到面的距离即可.
(1)证明:由题意,连接AC,如下图所示:
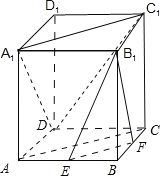
∵E是AB的中点,F是BC的中点,
∴EF∥AC,
∵四边形ACC1A1是平行四边形,
∴AC∥A1C1,
∴EF∥A1C1,
∵A1C1平面A1DC1,
∴EF∥平面A1DC1,即证.
(2)由题意,设长方体的高为h.
∵![]()
![]() 2
2![]() 2=2,
2=2,
∴![]()
![]()
![]()
![]() h
h![]() h.
h.
∵S△BEF![]()
![]() 1
1![]() 1
1![]() ,
,
∴![]()
![]() S△BEF
S△BEF![]() h
h![]()
![]()
![]()
![]() h
h![]() h.
h.
∵![]() 2
2![]() 2
2![]() h=4h,
h=4h,
∴4h![]() h
h![]() h
h![]() h
h![]() ,
,
解得h=2![]() .
.
又∵EF![]() ,DE=DF
,DE=DF![]() ,
,
容易知S△DEF![]() .
.
∴![]()
![]() S△DEF
S△DEF![]() B1B
B1B![]()
![]()
![]()
![]() 2
2![]() .
.
∵EF![]() ,B1E=B1F
,B1E=B1F![]() ,
,
∴![]() S△DEF
S△DEF![]() .
.
设点D到平面B1EF的距离为d.
∵![]() ,
,
∴![]()
![]()
![]()
![]() d
d![]() ,
,
解得d=2![]() .
.
∴点D到平面B1EF的距离为2![]() .
.

 中考解读考点精练系列答案
中考解读考点精练系列答案【题目】自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)现随机抽取1名顾客,试估计该顾客年龄在[30,50)且未使用自由购的概率;
(2)从被抽取的年龄在[50,70]使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在[50,60)的概率;
(3)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?