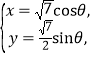题目内容
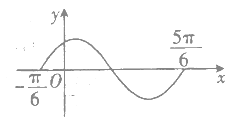
【题目】如图所示的是函数![]() (
(![]() ,
,![]() )在区间
)在区间![]() 上的图象,将该函数图象各点的横坐标缩小到原来的一半(纵坐标不变),再向右平移
上的图象,将该函数图象各点的横坐标缩小到原来的一半(纵坐标不变),再向右平移![]() (
(![]() )个单位长度后,所得到的图象关于直线
)个单位长度后,所得到的图象关于直线![]() 对称,则
对称,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】分析:由周期求出ω,由五点法作图求出![]() 的值,可得函数的f(x)的解析式.再根据函数g(x)的对称轴求出m的最小值,可得结论.
的值,可得函数的f(x)的解析式.再根据函数g(x)的对称轴求出m的最小值,可得结论.
详解:由函数![]() (
(![]() ,
,![]() )的图象可得
)的图象可得
T=![]()
再由五点法作图可得 2×(﹣![]() )+
)+![]() =0,∴
=0,∴![]() =
=![]() .
.
故函数f(x)的解析式为 f(x)=sin(2x+![]() ).
).
故把f(x)=sin(2x+![]() )的图象各点的横坐标缩小到原来的一半(纵坐标不变),再向右平移m(m>0)个单位长度后,得到g(x)=sin(4x﹣4m+
)的图象各点的横坐标缩小到原来的一半(纵坐标不变),再向右平移m(m>0)个单位长度后,得到g(x)=sin(4x﹣4m+![]() )的图象,
)的图象,
∵所得图象关于直线![]() 对称,
对称,
∴4×![]() ﹣4m+
﹣4m+![]() =
=![]() +kπ,解得:m=
+kπ,解得:m=![]() ﹣
﹣![]() kπ,k∈Z,
kπ,k∈Z,
∴由m>0,可得当k=1时,m的最小值为![]() .
.
故答案为:C

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目